Books / Memoization / Chapter 1
Introduction to Memoization
Memoization is a technique for improving the performance of a certain category of algorithms. It works by saving and reusing previously computed results rather than recomputing them.
Memoization is an optimization technique to make algorithms run faster with space-time tradeoff: it uses extra space (memory) to improve run time. Algorithms using memoization store intermediate results in an array or a map often called the memoization table. The previously computed results are retrieved later when they are needed again. This eliminates the cost of recalculation and makes the algorithm run faster.
Memoization Pseudocode
The key idea of Memoization is to remember previously computed results and reuse them.
- When the function is called with certain arguments:
- Lookup the memoization table (hashmap) to check if the result already exists
- If the result exists, return it to caller and exit
- If the result does not exist, compute it, store it in the memoization table, return it to caller and exit
- Lookup the memoization table (hashmap) to check if the result already exists
Memoization Use Case
There’s a certain class of algorithms that work by breaking up a bigger problem into smaller sub-problems. They then calculate solutions to these sub-problems and combine to build up the final solution.
In such algorithms, when sub-problems overlap or reoccur, memoization can be used to store results of sub-problems to avoid calculating solution to any sub-problem twice.
If an algorithm doesn’t have overlapping sub-problems, memoization will not improve its performance.
Memoization in Action
You have probably heard of the Fibonacci numbers. It is sequence of numbers that starts at 0, 1, 1 and then each subsequent number is calculated as the sum of the two preceding numbers. So we get 0, 1, 1, 2 because (1+1=2) and then 0, 1, 1, 2, 3 because (1+2=3) and so on.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
Let’s write a program to compute the nth Fibonacci number. We know the equation looks like this:
fib(n) = fib(n-1) + fib(n-2) for n > 1
To calculate the nth Fibonacci, we can break it into two sub-problems: fib(n-1) and fib(n-2).
For example, to calculate the 7th Fibonacci number, using the above equation, we get:
fib(7) = fib(6) + fib(5)
How do we get to fib(6) and fib(5)? We can break these up again and use recursion to calculate these:
fib(6) = fib(5) + fib(4)
and,
fib(5) = fib(4) + fib(3)
Fibonacci Numbers Using Recursion
Let’s write a simple algorithm in JavaScript to calculate the Fibonacci numbers using recursion:
function fibonacci(num) {
if (num <= 2) {
return 1
}
return fibonacci(num-1) + fibonacci(num-2) // recursive call
}
let num = 7
for (let i = 1; i<=num; i++) {
console.log("fibonacci(" + i + ") = " + fibonacci(i));
}
Our program starts at 1 and keeps calling the fibonacci(num) function in a loop to calculate Fibonacci numbers of 1 through num.
The function fibonacci(num) uses recursion to calculate the nth Fibonacci number:
fibonacci(num-1) + fibonacci(num-2)
Let’s visualize our algorithm for 7th Fibonacci number:
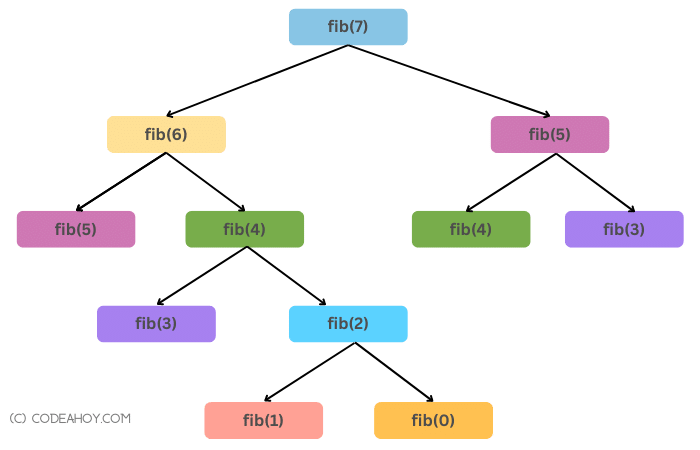
Tree diagram for calculating the 7th Fibonacci number.
In the diagram above, we can make a key observation:
- We can clearly see overlapping sub-problems:
fib(5)andfib(4)are evaluated twice andfib(3)is evaluated 3 times (not shown in the diagram).
In other words, each call to fibonacci(num) gives birth to two more function calls and there’s a lot of repetitive calculations.
For bigger numbers, fibonacci(num) will be dreadfully slow. Computing 40th Fibonacci number will result is:
- 8 calls to
fibonacci(35) - 13 calls to
fibonacci(34) - 21 calls to
fibonacci(33) - …
Our algorithm is clearly not at all efficient. But as we’ve been learning in tutorial, it has repeated sub-problems. Let’s improve its performance using Memoization in the next section.
Fibonacci Numbers Using Recursion with Memoization
As we noted in the last section, our Fibonacci number algorithm is not very efficient. One pattern that noted is that it recalculates results to sub-problems many time. As we have learned, this is where we can apply the Memoization technique to optimize our algorithm and improve its performance.
const fibonacciWithMemoization = function(num) {
const memoTable = []; // Memoization table for storing sub-problems / intermediate results
function fibonacci(num) {
if (num <= 2) {
return 1
}
// check if the num exists in the memoization table
if (memoTable[num]) {
return memoTable[num]; // return num
}
memoTable[num] = fibonacci(num-1) + fibonacci(num-2) // recursive call
return memoTable[num];
}
return fibonacci(num);
};
let num = 7
for (let i = 1; i<=num; i++) {
console.log("fibonacciWithMemoization(" + i + ") = " + fibonacciWithMemoization(i));
}
Time Complexity Analysis
Run the two algorithms above to find the 38th Fibonacci number and notice the CPU time. Here are the execution times:
- Fibonacci without Memoization: 3.24 seconds
- Fibonacci with Memoization: 0.06 seconds
That’s a huge improvement. We algorithm with simple Memoization ran 98% faster! In fact, using Memoization, we reduced the time complexity from O(2^n) to linear time complexity O(N).
The original Fibonacci algorithm had an exponential time complexity of O(2^n). This is because each node has makes two call. So we start at 1 level, then 2, then 4 and so forth. So it’s 2*2*2... = 2^n. This is what the tree looks like for 5th Fibonacci number.
With Memoization, we are reusing results from previous runs so our tree looks like this:
The ones with underline are just returning memoized results. You can see that the tree is linear and hence the time complexity is O(N).
Conclusion
In conclusion, memoization is a optimization technique for improving the performance of algorithms by storing previously computed results and reusing them later when needed. By avoiding the cost of recalculation of sub-problems when it encounters them again, memoization makes algorithms run faster, though it requires extra space. This technique is particularly useful in algorithms that break a bigger problem into smaller sub-problems and calculate solutions to these sub-problems, with overlapping or recurring sub-problems benefiting the most from memoization. The Fibonacci numbers problem is an example of an algorithm that can be significantly optimized by using memoization. The implementation of the Fibonacci algorithm using recursion is inefficient due to repetitive calculations, but memoization can help avoid redundant calculations and improve its performance.
Memoization is an optimization technique for improving the performance of recursive algorithms without having to change the way the algorithm works. Memoized algorithms store results of smaller sub-problems and ensure that no sub-problem is calculated twice. It is very useful in the context of Dynamic Programming.
Q&A
What is memoization?
Memoization is an optimization technique used to improve the performance (speed) of certain algorithms by saving and reusing previously computed results rather than recomputing them.
When should you use memoization?
Memoization is useful when an algorithm breaks up a bigger problem into smaller sub-problems, and those sub-problems overlap or reoccur. By storing the results of these sub-problems, memoization can avoid recalculating solutions and improve the algorithm’s performance.
What is the space-time tradeoff in memoization?
Memoization uses extra space (memory) to improve run time. By storing previously computed results in an array or map, memoization eliminates the cost of recalculation and makes the algorithm run faster at the cost of using extra space to store results.
What is recursion?
Recursion is a programming technique in which a function calls itself within its own definition to solve a problem. It is commonly used to break a problem down into smaller sub-problems that can be solved more easily.
When is memoization not a good choice?
Memoization is not a good choice when the function being memoized has a very large number of possible inputs, as this can result in a very large cache that may use up too much memory. Additionally, memoization is not effective when the function does not have overlapping subproblems or when the inputs change frequently.
If an algorithm doesn’t have overlapping sub-problems, will memoization help or have the opposite effect?
Memoization will not have any effect on the algorithm if it does not have overlapping sub-problems. Worse case, you’ll be using extra space to store results in the cache that are never re-used again. Since memoization is a technique for storing the results of expensive function calls and returning the cached result when the same inputs occur again, it requires the existence of overlapping sub-problems in the algorithm.
Is memoization the same as caching?
Memoization and caching are related concepts but are not the same.
Memoization is an optimization technique which is used in dynamic programming where a function’s result is stored in memory so that if the function is called again with the same input, the result can be retrieved from memory. This results in significant performance improvements in some algorithms.
Caching, on the other hand, is a more general concept where the result of an operation is stored in memory for future use. Caching can be used for many different types of operations, not just functions. For example, a web browser might cache images or web pages or other assets to speed up page loading times.
In summary, memoization is a specific type of caching that is used in dynamic programming to improve the efficiency by reducing the number of calls to compute expensive results.







