Dynamic Markov Compression is an obscure form of compression that uses Markov chains to model the patterns represented in a file.

Markov Chains

Markov Chains are a simple way to model the transitions between states based on a measurable probability. For example, we could use a Markov Chain to model the weather and the probability that it will become sunny if it’s already raining, or vice-versa.

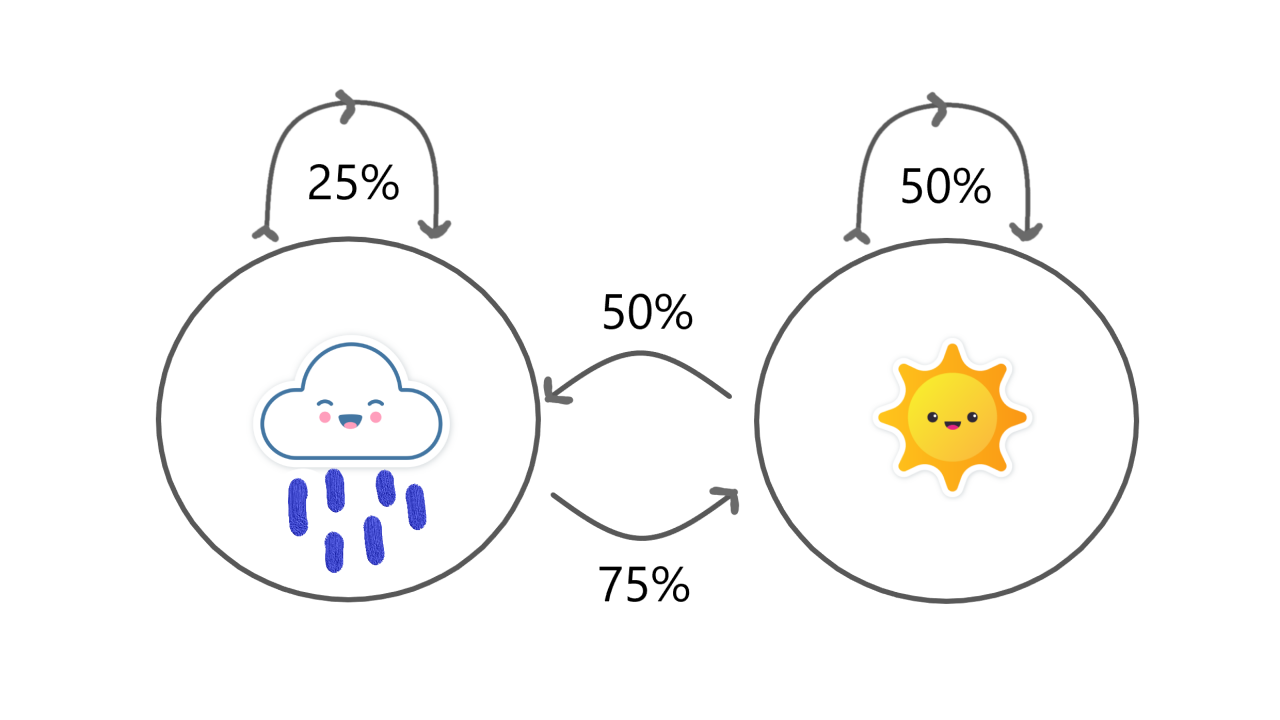
Each circle represents a state, and each arrow represents a transition. In this example, we have two states, raining and sunny, a perfect representation of true weather. Each state has two possible transitions, it can transition to itself again or it can transition to another state. The likelihood of each transition is defined by a percentage representing the probability that the transition occurs.

Now let’s say it’s sunny and we’re following this model. According to the model there’s a 50% chance it’s sunny again tomorrow or a 50% chance it’s rainy tomorrow. If it becomes rainy, then there’s a 25% chance it’s rainy the day after that or a 75% chance it’s sunny the day after that.

Markov Chains may sound scary but the essence of how they work is quite simple. Markov Chains are the statistical model behind a lot of the technology we use today from Google’s PageRank search algorithm to predictive text on smartphone keyboards. If you’d like to learn more, check out this wonderful article by Victor Powell and Lewis Lehe that goes into depth about how Markov Chains work. They also have a wonderful interactive demo.

Resources

If you’re interested in trying to implement DMC yourself or are just interested in the algorithm, here’s a few helpful resources as a jumping-off point:

• Dynamic Markov Compression on Wikipedia
• An Exploration of Dynamic Markov Compression Thesis
• The structure of DMC (Paywall)
• Original Paper
• Original C Implementation by Gordon Cormack
• Markov Chain Compression - Compressor Head
• Markov Chains

---

---