Books / Priority Queue / Chapter 4.1
Priority Queue Algorithms - Insertion
In all of the code that follows, we assume that the heap class is defined as a template class whose element type is a Comparable. In other words, it is of the form
template <class Comparable>
class heap {
public:
// all public methods here
private:
Comparable array[MAX_SIZE+1];
int current_size;
};
We do not provide a full description of the public interface to this class, nor do we provide implementations of its constructors, destructors, and various other methods. Instead we concentrate on the three important algorithms: inserting into a heap, deleting the minimum element, and building a heap. Obviously, obtaining the minimum element is trivial, as it is just array, so this is not discussed either. Our version of deleteMin does not return the minimum element, but it is an easy change to do that.
Insertion
The algorithm to insert a new item into a heap is simple: we put the element at the end of the array, i.e., after the last item currently in the array, which, viewed as a binary tree, is in the bottom-most level to the right of the rightmost key. If the tree is full, the new item starts a new level. The tree may not be a heap anymore, because the item may be smaller than its parent. Therefore, we need to check if this is true and restore the heap order property. To make this clear, suppose that the data is in an array named array, that it has current_size elements, and that the item was just inserted into position \(\mathrm{k}=\) current_size+1. Then the following code snippet will correct this problem:
if (array[k] < array[parent(k)]) {
swap(array[k], array[parent(k)]);
}
Since \(\operatorname{parent}(k)\) is just \(k / 2\), this simplifies to
if (array[k] < array[k/2] ) {
swap(array[k], array[k/2]);
}
If the child was swapped with its parent, it is possible, that it is also smaller than its new parent, i.e., what was its grandparent before the swap. So this is repeated. In fact it may need to repeat all the way back to the root of the heap. This suggests that we need code of the form
current_size++; // increment the size of the array
k = current_size;
while ( array[k] < array[k/2] ) {
swap(array[k], array[k/2]);
k = k/2;
}
But this has a problem, because it fails to check whether k has reached the root (i.e., whether k==1 ). so it should be
current_size++; // increment the size of the array
k = current_size;
while ( (k > 1) && array[k] < array[k/2] ) {
swap(array[k], array[k/2]);
k = k/2;
}
Finally, it is silly to keep swapping the element upward. Instead we can just keep it in a variable, say new_item, and “slide” the parents into the hole that it creates when it would be swapped. The algorithm that does this is called upward percolation. Upward percolation is the act of upwards percolate it up to the top as far as necessary to restore the heap-order. Suppose that the heap stores its data in an array named array, and that current_size is the current size of that array. Assume that we have functions to check if the array is full. Then our insert function becomes the following.
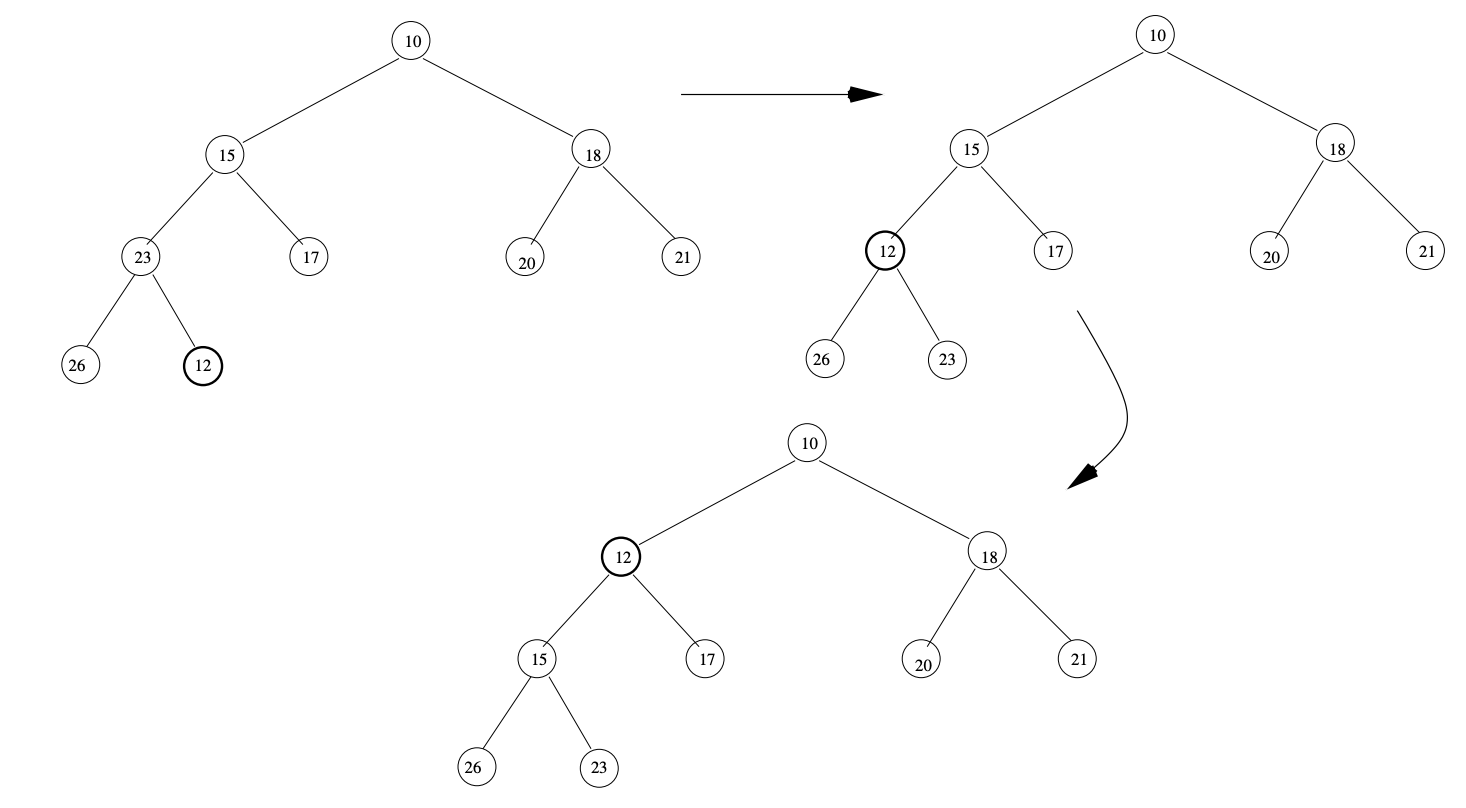
Figure 3 -Inserting into a heap
template < class Comparable >
void heap < Comparable >:: insert ( const Comparable & new_item ) {
if (isFull ()) {
throw Overflow ( ) ;
}
// Percolate up
int hole = ++ current_size ;
while ( hole > 1 && new_item < array [ hole /2] ) {
array [ hole ] = array [ hole / 2 ];
hole = hole /2;
}
array [ hole ] = new_item ;
}
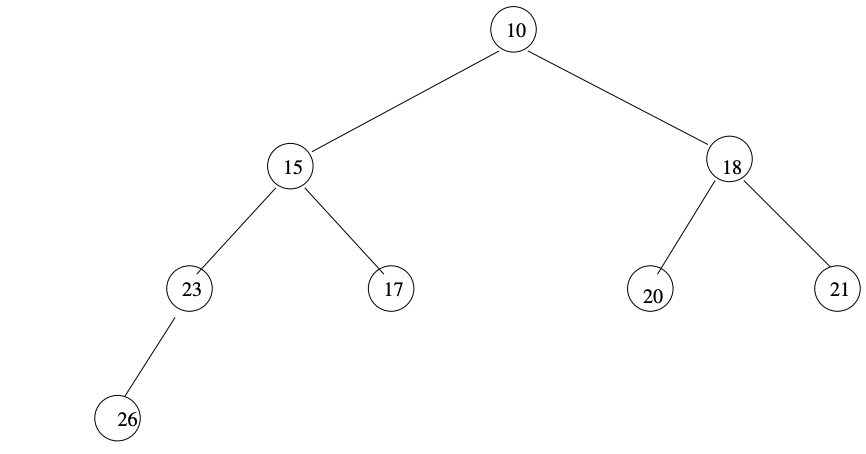
Figure 3 shows how the insertion algorithm behaves when items are inserted into the heap from Figure 1 from Chapter 4 which is reproduced below: