Books / Priority Queue / Chapter 4.2
Priority Queue Algorithms - Deleting the Minimum Element
In all of the code that follows, we assume that the heap class is defined as a template class whose element type is a Comparable. In other words, it is of the form
template <class Comparable>
class heap {
public:
// all public methods here
private:
Comparable array[MAX_SIZE+1];
int current_size;
};
The deleteMin algorithm is also very easy to implement. To delete the smallest element, we remove the root. Now there is a hole where the root used to be. We take the last element of the heap, meaning the rightmost leaf in the bottom level, and put it where the root was. It might be bigger than its children though, so we have to handle this problem. We pick the smaller of the two children and swap it with the root. We must pick the smaller, otherwise we would be destroying the heap-order property, because the larger child would be the parent of the smaller child. We need to repeat this until either the element is smaller than both of its children, or it has been swapped down until it became a leaf node. This process, in which an element that is too big for its position in the heap is repeatedly pushed down in the heap until it settles on top of a subtree whose elements are all larger than it, is called downward percolation. Because downward percolation is an algorithm that is used in other methods for maintaining a heap, we make it a helper function, as follows:
// hole is the position containing an element that might need to be
percolated down
template < class Comparable >
void heap < Comparable > ::percolateDown(int hole) {
int child;
Comparable temp = array[hole]; // copy the element for later
insertion
while (2 * hole <= current_size) {
child = hole * 2; // left child of hole
if (child != current_size && array[child + 1] < array[child])
// right child exists and is smaller than left , so make child
its index
child++;
if (array[child] < temp)
// copy smaller child into hole
array[hole] = array[child];
else
break; // both children are bigger than hole
// repeat with hold being child that was copied up
hole = child;
}
array[hole] = temp;
}
Now the deleteMin function is easy:
template < class Comparable >
void heap < Comparable > ::deleteMin()
// or you can make it
// void heap < Comparable >:: deleteMin ( Comparable & min_item )
// and set min_item = array [1]
{
if (isEmpty())
throw Underflow();
array[1] = array[current_size];
current_size - -;
percolateDown(1);
}
Example Figure 4 illustrates how the deleteMin algorithm works. The root element is replaced by the last element, in this case 23 . Then the percolateDown function is called to move 23 into the position in which it belongs. Because 12 is the smaller of its two children, 12 is moved to the root. Then 23 is compared to 15 and 17, and 15 , the smaller, is moved up. Since the hole that 15 left has just a single child, 26 , and \(23<26,23\) is inserted into the hole.
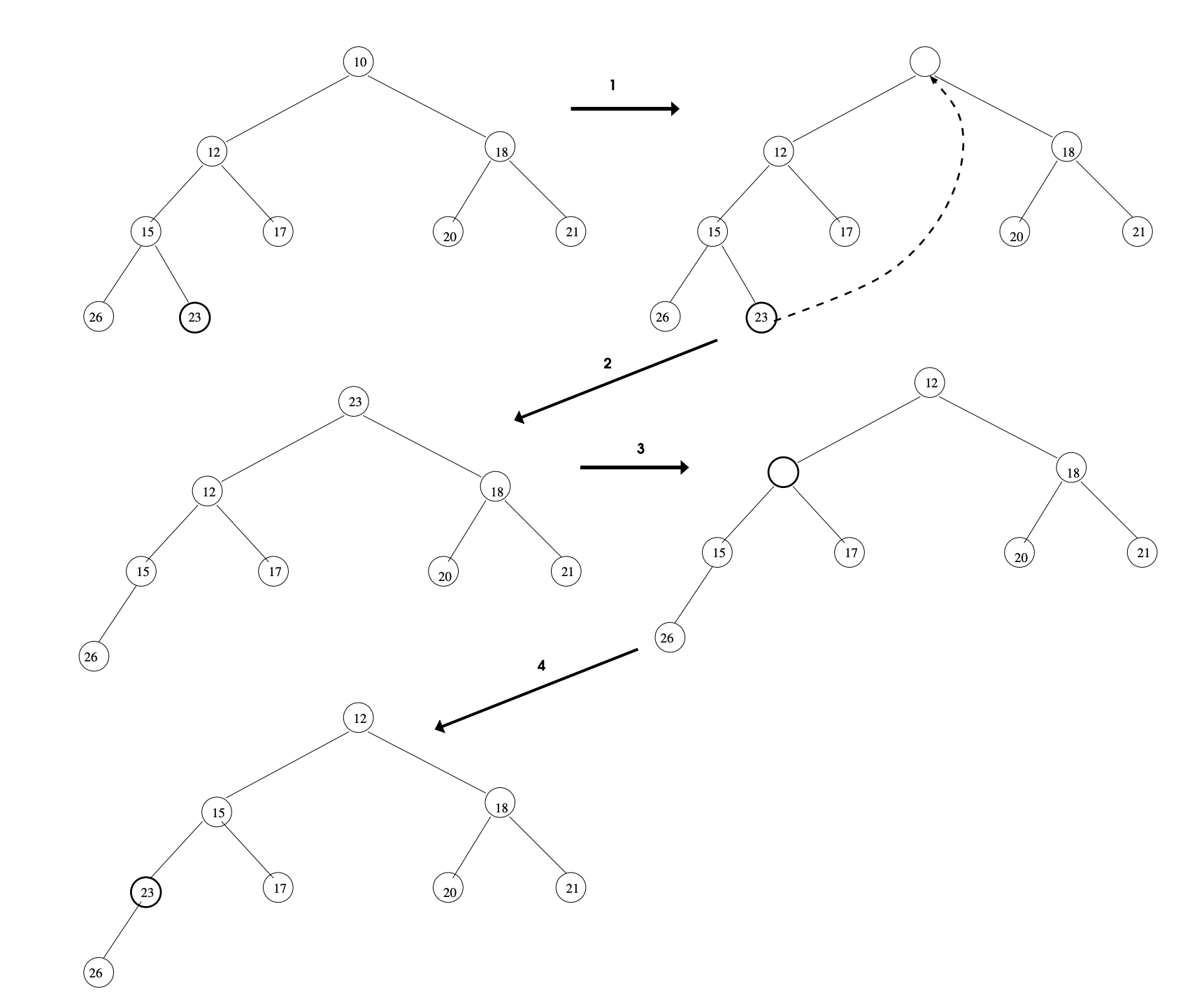
Figure 4: The deleteMin operation applied to the tree from Figure 3



