Depth First Search (DFS)

Depth-first search (or DFS for short) is a very common and natural way of traversing a graph (either directed or undirected) or a tree. The DFS algorithm starts usually at the root vertex or node (vertex and node mean the same thing) and then visits all nodes adjacent or connected to it that have not been visited. It picks a node and goes as far as it can until there are no more nodes to visit before backtracking. To prevent the algorithm from going into an endless loop by revisiting nodes, when a node is visited for the first time it is marked.

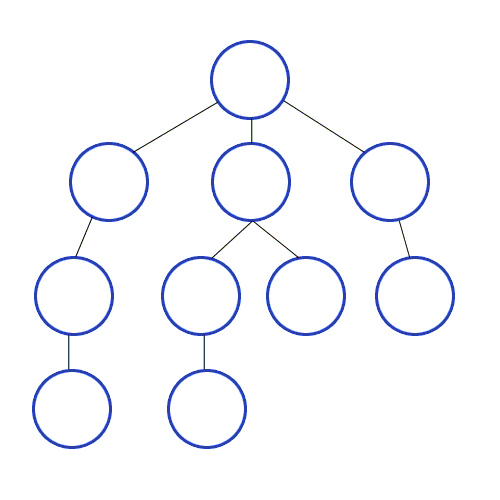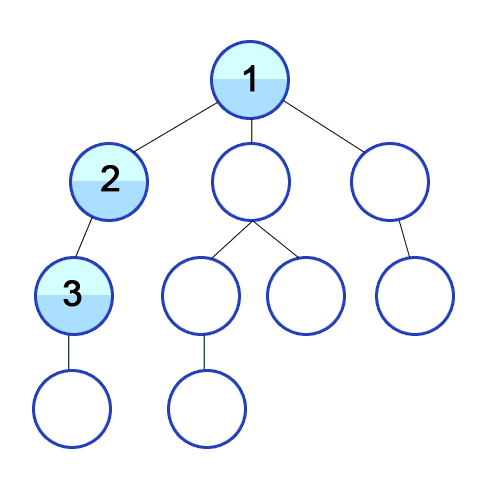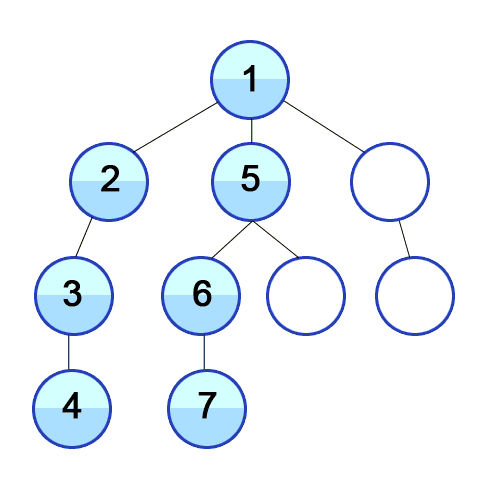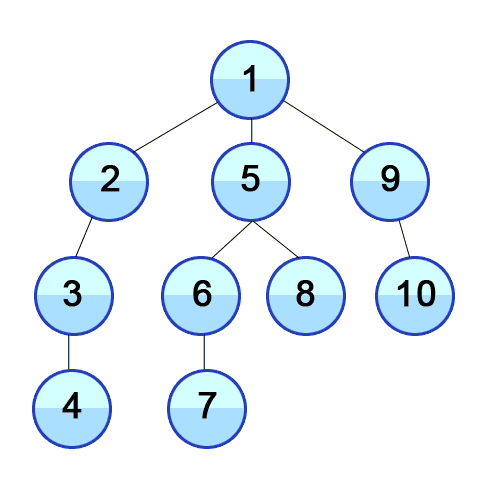
DFS animation showing the order in which nodes are traversed. Source: “Animated example of a depth-first search”, from Wikipedia.

Traversing Using DFS

Suppose we have the following directed graph.

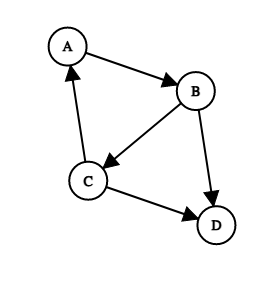
4-Node Graph with cycles that we'll use in our examples. — 4-Node Graph with cycles that we’ll use in our examples.

The DFS algorithm starts at the root vertex A. It visits it and adds it to the visited set.
The algorithm follows the edge from A->B to visit vertex B and adds it to the visited set.
B has two neighbors: C and D. It arbitrarily picks up the edge from B->C and visits vertex C. It adds vertex C to the visited set.
It follows the edge from C->A. Upon arriving it A, it realizes it has visited it already so it backtracks to C to visit its next neighbor.
It then follows the edge from C->D and adds D to the visited set since it hasn’t visited it before.
It then backtracks to C and then to B. It follows the remaining edge from B->D. However, upon arriving at D, it realizes that it has visited it already.
The backtracking continues and the algorithm ends since it has visited all the vertices.

Time Complexity of DFS

The time complexity of DFS algorithm depends on the specific implementation and the characteristics of the graph or tree which it is traversing.

Best Case

In the best case, DFS has a time complexity of O(V). If the graph is a tree (i.e. has no cycles and each node has exactly one parent node, except for the root) then the algorithm only needs to visit the vertices of the graph, and not the edges. In this case, the time taken is directly proportional to the number of vertices in the graph.

Worst Case

In the worst case, DFS has a time complexity of O(V + E), where V is the number of vertices (or nodes) in the graph and E is the number of edges. This is because the DFS algorithm will need to visit some nodes and edges more than once so it could explore the entire graph.

The DFS algorithm we explored above visited every node and every edge. In total, it visited 4 vertices and 5 edges. Therefore, the time complexity of the algorithm is:

O(V + E) = O(4 + 5) = O(9)

Where V is the number of vertices (or nodes) in the graph and E is the number of edges

In general, the time complexity of DFS is O(V + E), but it can be as good as O(V) if the graph is a tree.

The worst-case space complexity if O(V) since it needs to store the set of visited vertices or a stack of vertices.

# 1. DFS pseudocode implementation using recursion

# This function takes as input a graph, a vertex (node), and a visited set. If the vertex 
# is not already visited, it recursively calls itself on each of the neighbors of the  vertex
def DFS(graph, vertex, visited):
  if vertex not in visited:
    print(vertex)
    visited.add(vertex)
    for neighbor in graph[vertex]:
      DFS(graph, neighbor, visited)

# This function is initializes the visited set and calls the DFS() function with 
# the root node. It returns the visited set after the recursive calls have completed.
def Initialize(graph, start):
  visited = set() # empty set
  DFS(graph, start, visited)

## Graph from Figure 2
graph = {
    'A' : ['B'],
    'B' : ['C', 'D'],
    'C' : ['A', 'D'],
    'D' : []
}

Initialize(graph, 'A')

# Output
# A
# B
# C
# D


# 2. Iterative DFS without recursion

# The DFS function uses a stack to keep track of which nodes to visit next. It starts at 
# the root node and adds it to the visited set. It then follows the edges of the graph, 
# visiting each neighbor of the current node and adding it to the stack. The algorithm 
# continues this process until the stack is empty, at which point it returns the visited set.

def DFS_Iterative(graph, start):
  visited = set()
  stack = [] # empty stack
  stack.append(start)
  while len(stack) != 0:
    vertex = stack.pop()
    if vertex not in visited:
      print(vertex)    
      visited.add(vertex)
      for neighbor in graph[vertex]:
        stack.append(neighbor)
  return visited

Depth First Search (DFS)

Traversing Using DFS

Time Complexity of DFS

Best Case

Worst Case

Related Tutorials

DFS Applications

Depth-First Search

Graphs

Graph Traversals - Depth First Search Algorithm

Related Videos