Graph Traversals - Depth First Search Algorithm

Depth-first Search

A very common and natural way to traverse a graph, directed or undirected, is analogous to a pre-order traversal of a binary tree and it is called a depth-first search, or DFS for short. DFS is a backtrack-style traversal that visits a node and then recursively visits all nodes adjacent to it that have not yet been visited. To prevent the algorithm from going into an endless loop by revisiting nodes, when a node is visited for the first time it is marked.

Here’s an animation showing Depth-first search.

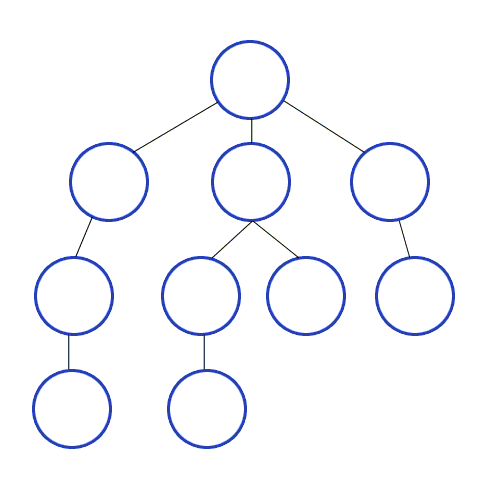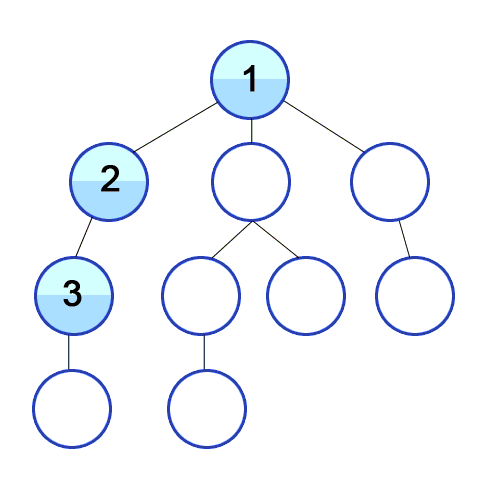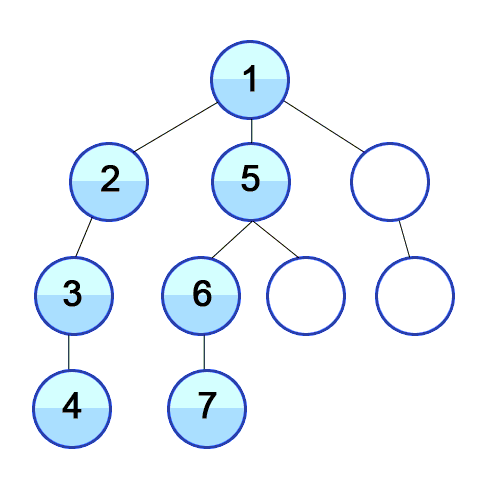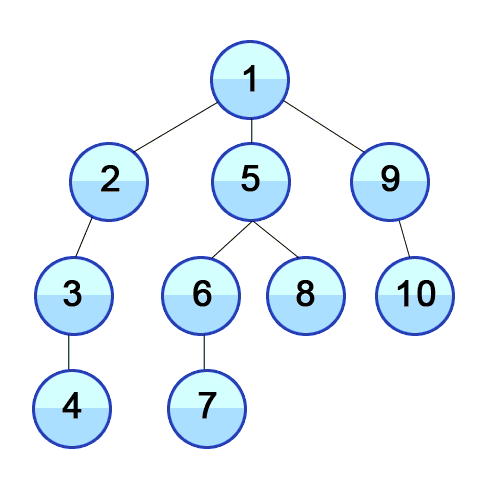
DFS Algorithm

DFS is typically implemented using a Stack to store the vertices. Let’s start by looking at some simple pseudo code.

DFS(s):
    put s into the stack
    while the stack is not empty
        take v from the bag
        if v is unmarked
            mark v
        for each edge vw
            put w into the stack

Depth-first search will marks every node reachable from s and nothing else. The algorithm clearly marks each vertex in G at most once.

Here’s a little more concrete, yet still general algorithm that does nothing other than traverse the graph is:

for all vertices v in V { // mark all vertices as unvisited
    v.visited = false;
}

void Graph::DFS( Vertex v) {
    v.visited = true;
    for each vertex w that is adjacent to v {
        if ( !w.visited) {
            DFS(w);
        }
    }
}

If an undirected graph is not connected, this will not visit every node. Similarly, if a directed graph is not strongly connected, it will not visit every node. The solution is to use a numbering scheme. Initially every vertex will have its number set to 0 . When it is visited by DFS, it will get a non-zero number. If after processing all vertices, some still have zero as their number, they were not visited and must be in a part of the graph that was not connected to where the DFS started. DFS can be called for each vertex whose number is zero. The following C++ algorithm illustrates this idea and also introduces the concept of tree edges and back edges.

void Graph::DFS(Vertex v, Vertex u) {
  // u is the parent of v in the search , i.e., (u , v) is the edge
  i += 1;
  v.number = i;
  for all w adjacent to v {
    if (w.number == 0) {
      // this is a tree edge
      Tree_edges = Tree_edges + (v, w);
      DFS(w, v);
    } else if (w.number < v.number && w != u) {
      // this is a back edge
      Back_edges = Back_edges + (v, w);
    }
  }
}
// Assume that 0 represents a non - existent node i.e., all nodes have labels greater than 0
void Graph::DFS() {
  i = 0;
  Tree_edge = {};
  Back_edges = {};
  for all v in V {
    v.number = 0;
  }
  for all v in V {
    if (v.number == 0) {
      DFS(v, 0);
    }
  }
}

DFS Complexity or Performance Analysis

If we build DFS using a stack, that supports insertions (push) and deletions (pop) in O(1) time each, the algorithm runs in O(V + E) time. The for loop (†) is executed exactly once for each marked vertex, and therefore at most V times. Each edge uv is put into the stack exactly twice; once as the pair (u, v) and once as the pair (v, u), so it is executed 2E times. This assumes that the graph is represented using adjacency lists.