Exclusive or, often called “XOR”, is a Boolean¹ binary² operator that is true when either the first input or the second input, but not both, are true.

Another way to think of XOR is as something called a “programmable inverter”: one input bit decides whether to invert the other input bit, or to just pass it through unchanged. “Inverting” bits is colloquially called “flipping” bits, a term we'll use often throughout the book.

In mathematics and cryptography papers, exclusive or is generally represented by a cross in a circle: ⊕. We'll use the same notation in this book:

The inputs and output here are named as if we're using XOR as an encryption operation. On the left, we have the plaintext bit \(P_i\). The \(i\) is just an index, since we'll usually deal with more than one such bit. On top, we have the key bit \(k_i\), that decides whether or not to invert \(P_i\). On the right, we have the ciphertext bit, \(C_i\), which is the result of the XOR operation.

A few properties of XOR

Since we'll be dealing with XOR extensively during this book, we'll take a closer look at some of its properties. If you're already familiar with how XOR works, feel free to skip this section.

We saw that the output of XOR is 1 when one input or the other (but not both) is 1:

There are a few useful arithmetic tricks we can derive from that.

1. XOR can be applied in any order: \(a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c\)
2. The operands can be flipped around: \(a ⊕ b = b ⊕ a\)
3. Any bit XOR itself is 0: \(a ⊕ a = 0\). If \(a\) is 0, then \(0 ⊕ 0 = 0\); if \(a\) is 1, then \(1 ⊕ 1 = 0\).
4. Any bit XOR 0 is that bit again: \(a ⊕ 0 = a\). If \(a\) is 0, then \(0 ⊕ 0 = 0\); if \(a\) is 1, then \(1 ⊕ 0 = 1\).

These rules imply that \(a ⊕ b ⊕ a = b\):

We use this property for XOR encryption. The first XOR \(a\) can be thought of as encrypting, and the second one as decrypting.

Bitwise XOR

XOR, as we’ve just defined it, operates only on single bits or Boolean values. Since we usually deal with values comprised of many bits, most programming languages provide a “bitwise XOR” operator: an operator that performs XOR on the respective bits in a value.

As an example, Python has the ^ (caret) operator performing bitwise XOR on integers. It first expresses two integers in binary³, and then performs XOR on their respective bits. Hence the name, bitwise XOR.

One-time pads

XOR may seem like an awfully simple, even trivial operator. Even so, there is an encryption scheme. It is called a one-time pad, which consists of a single operator with a sequence (“pad”) of random bits. The security of the scheme depends on using the pad only once. The sequence is called a pad because it was originally recorded on a physical, paper pad.

The scheme is unique not only in its simplicity. It has the highest security guarantee possible. If the bits are truly random, they become unpredictable for an attacker. Additionally, if the pad is only used once, the attacker learns nothing about the plaintext when viewing a ciphertext.⁴

Suppose we can translate our plaintext into a sequence of bits. We also have the pad of random bits, shared between the sender and the (one or more) recipients. We can compute the ciphertext by taking the bitwise XOR of the two sequences of bits.

If an attacker sees the ciphertext, we can prove that zero information is learned about the plaintext without the key. This property is called perfect secrecy. The proof can be understood intuitively. Think of XOR as a programmable inverter, and look at a particular bit intercepted by Eve, the eavesdropper.

Let's say Eve sees that a particular ciphertext bit \(c_i\) is 1. She has no idea if the matching plaintext bit \(p_i\) was 0 or 1, because she has no idea if the key bit \(k_i\) was 0 or 1. Since all of the key bits are truly random, both options are exactly equally probable.

Attacks on “one-time pads”

The one-time pad security guarantee only holds if used correctly. First of all, the one-time pad must consist of truly random data. Secondly, the one-time pad can only be used once (hence the name). Unfortunately, most commercial products that claim to be “one-time pads” are snake oil⁵, and do not satisfy at least one of these two properties.

Not using truly random data

The first issue is that various deterministic constructs produce the one-time pad instead of using truly random data. That is not necessarily insecure: in fact, the most obvious example, a synchronous stream cipher, is something we will see later in the book. However, it does invalidate the “unbreakable” security property of one-time pads. The end user is better served by a more honest cryptosystem, not one that lies about its security properties.

Reusing the “one-time” pad

The other issue is with key reuse, which is much more serious. Suppose an attacker gets two ciphertexts with the same “one-time” pad. The attacker can then XOR the two ciphertexts, which is also the XOR of the plaintexts:

At first sight, that may not seem like an issue. To extract either \(p_1\) or \(p_2\), you'd need to cancel out the XOR operation, which means you need to know the other plaintext. The problem is that even the result of the XOR operation on two plaintexts contains quite a bit information about the plaintexts themselves. 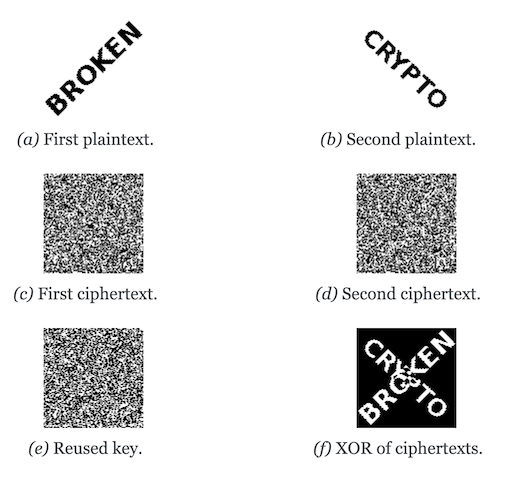We’ll illustrate this visually with some images from a broken “one-time” pad process, starting with Figure 1.

Two plaintexts, the re-used key, their respective ciphertexts, and the XOR of the ciphertexts. Plaintext information clearly leaks through when we XOR the ciphertexts.

Crib-dragging

A classic approach to break multi-time pad systems is “crib-dragging.” Crib-dragging uses small sequences expected to occur with high probability. Those sequences are “cribs”. The name crib-dragging originates from the fact that these small “cribs” are dragged from left to right across each ciphertext, and from top to bottom across the ciphertexts, in the hope of finding a match. The matches form the sites of the start, or “crib”, if you will, of further decryption.

The idea is fairly simple. Suppose we have several encrypted messages \(C_i\) encrypted with the same “one-time” pad \(K\) ⁶. If we could correctly guess the plaintext for one of the messages, let's say \(C_j\), we'd know \(K\):

Since \(K\) is the shared secret, we can use it to decrypt all other messages as if we are the recipient:

This typically does not work because we cannot guess an entire message. However, we can guess parts of a message.

If we guess a few plaintext bits \(p_i\) correctly for any of the messages that reveals the key bits at that position for all of the messages since \(k = c_i ⊕ p_i\). Hence, all of the plaintext bits at that position are revealed. Using that value for \(k\), we can compute the plaintext bits \(p_i = c_i ⊕ k\) for all the other messages.

Guessing parts of the plaintext is easier than guessing the entire plaintext. Suppose we know that the plaintext is in English. There are sequences that will occur very commonly. For example (the symbol denotes a space):

• and variants such as

• and variants

• and variants

• (no variants; only occurs in the middle of a sentence)

• and variants

We can make better guesses if more information is known about the plaintext. For example, if HTML is served over HTTP we expect to see Content-Type, <a>, and so on.

This only tells us which plaintext sequences are likely, giving us likely guesses. How can we tell if the guesses are correct? If our guess is correct, we know all the plaintexts at that position based on using the technique described earlier. We can simply look at those plaintexts and decide if they look correct.

In practice, the process needs to be automated because of all potential guesses. Fortunately that is easy to do. For example, a simple but effective method is to count how often different symbols occur in the guessed plaintexts: if the messages contain English text, we expect to see a lot of letters e, t, a, o, i, n. If we see binary nonsense instead, we know that the guess was probably incorrect, or perhaps that message is actually binary data.

These small, highly probable sequences are known as “cribs” because they are the start of a larger decryption process. Suppose your crib, the, was successful and found the five-letter sequence t thr in another message. You can use a dictionary to find common words starting with thr, such as through. If that is a correct guess, it can reveal four more bytes in all of the ciphertexts. This information can be useful for revealing more. Similarly, you can use the dictionary to find words ending in t.

This becomes greatly effective for plaintexts that we know more about. If HTTP data has the plaintext ent-Len, then we can expand that to Content-Length:. More bytes are easily revealed.

While this technique works as soon as two messages are encrypted with the same key, it is clear that the process becomes simpler when more ciphertexts use the same key. Since all of the steps become more effective we get:

• More cribbing positions.
• More plaintext bytes revealed with each successful crib and guess. This leads to more guessing options elsewhere.
• More ciphertexts available for any given position. This simplifies guess validation and at times increases accuracy.

We have reviewed simple ideas for breaking multi-time pads. While they are already quite effective, people invent more effective methods by applying advanced, statistical models using natural language analysis. This further demonstrates just how broken multi-time pads are.

Remaining problems

Real one-time pads, implemented properly, have an extremely strong security guarantee. It would appear, then, that cryptography is over: encryption is a solved problem, and we can all go home. Obviously, that is not the case.

One-time pads are rarely used for being horribly impractical. The key is at least as large as all information you would like transmitted, put together. Plus, the keys must be exchanged securely, ahead of time, with all people you would like to communicate with. We would like to communicate securely with everyone on the Internet, and that is a very large number of people. Furthermore, since the keys must consist of truly random data for the security property to hold, key generation is difficult and time-consuming without specialized hardware.

One-time pads pose a trade-off. An advantage is that a one-time pad is an algorithm with a solid information-theoretic security guarantee. The guarantee is not available with any other system. On the other hand, the key exchange requirements are extremely impractical. However, throughout this book, we will see that secure symmetric encryption algorithms are not the pain point of modern cryptosystems. Cryptographers designed plenty while practical key management is the toughest challenges facing modern cryptography. One-time pads may solve a problem, but it is the wrong problem.

One-time pads may have practical use, but they are obviously not a panacea. We need a system with manageable key sizes and capable of maintaining secrecy. Additionally, a system to negotiate keys over the Internet with complete strangers is necessary.

---

---