Stream ciphers

What are Stream ciphers?

A stream cipher is a symmetric-key encryption algorithm that encrypts a stream of bits. Ideally, that stream could be as long as we’d like; real-world stream ciphers have limits, but they are normally sufficiently large that they don’t pose a practical problem.

A naive attempt with block ciphers

Let’s try to build a stream cipher using the tools we already have. Since we already have block ciphers, we could simply divide an incoming stream into different blocks, and encrypt each block:

This scheme is called ECB mode (Electronic Code Book Mode), and it is one of the many ways that block ciphers can be used to construct stream ciphers. Unfortunately, while being very common in home-grown cryptosystems, it poses very serious security flaws. For example, in ECB mode, identical input blocks will always map to identical output blocks:

At first, this might not seem like a particularly serious problem. Assuming the block cipher is secure, it doesn’t look like an attacker would be able to decrypt anything. By dividing the ciphertext stream up into blocks, an attacker would only be able to see that a ciphertext block, and therefore a plaintext block, was repeated.

We’ll now illustrate the many flaws of ECB mode with two attacks. First, we’ll exploit the fact that repeating plaintext blocks result in repeating ciphertext blocks, by visually inspecting an encrypted image. Then, we’ll demonstrate that attackers can often decrypt messages encrypted in ECB mode by communicating with the person performing the encryption.

Visual inspection of an encrypted stream

To demonstrate that this is, in fact, a serious problem, we’ll use a simulated block cipher of various block sizes and apply it to an image¹. We’ll then visually inspect the different outputs.

Because identical blocks of pixels in the plaintext will map to identical blocks of pixels in the ciphertext, the global structure of the image is largely preserved.

As you can see, the situation appears to get slightly better with larger block sizes, but the fundamental problem still remains: the macrostructure of the image remains visible in all but the most extreme block sizes. Furthermore, all but the smallest of these block sizes are unrealistically large. For an uncompressed bitmap with three color channels of 8 bit depth, each pixel takes 24 bits to store. Since the block size of AES is only 128 bits, that would equate to \(\frac{128}{24}\) or just over 5 pixels per block. That’s significantly fewer pixels per block than the larger block sizes in the example. But AES is the workhorse of modern block ciphers—it can’t be at fault, certainly not because of an insufficient block size.

Notice that an idealized encryption scheme looks like random noise. “Looking like random noise” does not mean something is properly encrypted: it just means that we cannot inspect it using trivial methods.

Encryption oracle attack

In the previous section, we focused on how an attacker can inspect a ciphertext encrypted using ECB mode. That is a passive, ciphertext-only attack. It is passive because the attacker does not interfere in communications. The attacker simply examines the ciphertext. In this section, we study a different, active attack, where the attacker actively communicates with their target. We see how the active attack enables an attacker to decrypt ciphertexts encrypted using ECB mode.

To do this, we introduce a new concept called an oracle. Formally defined oracles are used in the field of computer science. For our purposes it is sufficient to say that an oracle computes a particular function.

Oracle: A “black box” that will perform some computation for you

In our case, the oracle performs a specific encryption for an attacker as an encryption oracle. Given some data \(A\) chosen by the attacker, the oracle encrypts that data, followed by a secret suffix \(S\), in ECB mode. Or, in symbols:

The secret suffix \(S\) is specific to this system. The attacker’s goal is to decrypt it. The ability to encrypt other messages surprisingly allows the attacker to decrypt the suffix. This oracle may seem artificial, but it is quite common in practice. A simple example is a cookie encrypted with ECB, where the attacker can control prefix \(A\) such as a name or an e-mail address field.

You can see why the concept of an oracle is important here: the attacker would not be able to compute \(C\) themselves, since they do not have access to the encryption key \(k\) or the secret suffix \(S\). The goal of the oracle is for those values to remain secret, but we’ll see how an attacker will be able to recover the secret suffix \(S\) (but not the key \(k\)) anyway. The attacker does this by inspecting the ciphertext \(C\) for many carefully chosen values of the attacker-chosen prefix \(A\).

Assuming that an attacker has access to such an oracle may seem like an artificial scenario. In practice, a lot of software can be tricked into behaving like one. Even if an attacker cannot control the real software as precisely as querying an oracle, the attacker is not thwarted. Time is on their side: they only have to convince the software to give the answer they want once. Systems where part of the message is secret and part of the message can be influenced by an attacker are very common, and, unfortunately, so is ECB mode.

Decrypting a block using the oracle

The attacker begins by sending in a plaintext \(A\) that is one byte shorter than the block size. This means that the block being encrypted consists of those bytes, plus the first byte of \(S\), which we can call \(s_0\). The attacker remembers the encrypted block. They do not know the value of \(s_0\), but they do know the value of the first encrypted block: \(E_k(A \| s_0)\). In the illustration, this is block \(C_{R1}\):

The attacker then tries all possible values for the final byte of a full-size block. The attacker eventually finds the value of \(s_0\); the guess is correct because the resulting ciphertext block matches the ciphertext block \(C_{R1}\) that was remembered earlier.

The attacker can repeat this strategy for the penultimate byte. A plaintext \(A\), two bytes shorter than the block size, is submitted. The oracle encrypts a first block containing \(A\) followed by the first two bytes of the secret suffix, \(s_0s_1\). The attacker remembers the block.

Since the attacker already knows \(s_0\), guessing begins from \(A \| s_0\) followed by all possible values of \(s_1\). Eventually the attacker’s guesses are correct, and the ciphertext blocks match:

The attacker rinses and repeats, eventually decrypting an entire block. This strategy allows brute-forcing a block in \(p \cdot b\) attempts, where \(p\) is the number of possible values for each byte (e.g. for 8-bit bytes that is \(2^8 = 256\)) and \(b\) is the block size. This aforementioned approach is better than a regular brute-force attack where an attacker tries all possible blocks which is:

For a typical block size of 16 bytes (or 128 bits) brute forcing means trying \(256^{16}\) combinations. The number of tries amounts to a huge, 39-digit number. It is so large that trying all combinations is impossible. An ECB encryption oracle allows an attacker to decrypt in at most \(256 \cdot 16 = 4096\) tries, which is a far more manageable number.

Conclusion

In the real world, block ciphers are used in systems that encrypt large amounts of data all the time. We see that when using ECB mode, an attacker both analyzes ciphertexts to recognize repeating patterns, and even decrypts messages when given access to an encryption oracle.

Even when we use idealized block ciphers with unrealistic properties, such as block sizes of more than a thousand bits, an attacker can decrypt the ciphertexts. Real world block ciphers have more limitations than our idealized examples, for example, having much smaller block sizes.

We are not yet even considering potential weaknesses in the block cipher. It is not AES nor the test block ciphers that cause the problem, it is our ECB construction. Clearly, something better is needed.

Block cipher modes of operation

A common way of producing a stream cipher is by using a block cipher in a particular configuration. The compound system behaves like a stream cipher. These configurations are known as mode of operations. They are not specific to a particular block cipher.

ECB mode, which we have just seen, is the simplest such mode of operation. The letters ECB stand for electronic code book². For reasons we already discussed, ECB mode is insecure. Fortunately, plenty of other choices exist.

CBC mode

CBC mode, cipher block chaining, is a common mode of operation. This operation involves XORing plaintext blocks with the previous ciphertext block before it is encrypted by the block cipher.

Of course, this process presents a problem for the first plaintext block: there is no previous ciphertext block to XOR it with. Instead, we select an IV: a random block in place of the “first” ciphertext. initialization vectors also appears in many algorithms. An initialization vector should be unpredictable, ideally, cryptographically random. IVs do not have to be kept secret: they are typically just added to ciphertext messages in plaintext. It may sound contradictory that an IV must be unpredictable, but not kept a secret. It is important to remember that an attacker should not be capable of predicting a given IV ahead of time. We illustrate this later with an attack on predictable CBC IVs.

The following diagram demonstrates encryption in CBC mode:

Decryption is the inverse construction. The block ciphers are in decryption mode instead of encryption mode:

While CBC mode is not inherently insecure (unlike ECB mode), its particular use was in TLS 1.0. This eventually led to the BEAST attack, which we detail in the SSL/TLS section. The short version is that instead of using unpredictable initialization vectors like random IVs, the previous ciphertext block was used as the IV for the next message. Unfortunately, attackers found out how to exploit this property.

Attacks on CBC mode with predictable IVs

Suppose there is a database storing secret user information, like medical, payroll or criminal records. The server protects the information by encrypting it with a strong block cipher in CBC mode with a fixed key. For now, we assume the server is secure, and no way for the key to leak.

Mallory gets a hold of all of the rows in the database. Perhaps she did it through a SQL injection attack, or maybe with a little social engineering.³ Everything is supposed to remain secure: Mallory only has the ciphertexts, but she doesn’t have the secret key.

Mallory wants to figure out what Alice’s record says. For simplicity’s sake, let’s say there’s only one ciphertext block. That means Alice’s ciphertext consists of an IV and one ciphertext block.

Mallory can still try to use the application as a normal user, meaning that the application will encrypt some data of Mallory’s choosing and write it to the database. Suppose that through a bug in the server, Mallory can predict the IV that will be used for her ciphertext. Perhaps the server always uses the same IV for the same person, or always uses an all-zero IV, or…

Mallory can construct her plaintext using Alice’s IV \(IV_A\) (which Mallory can see) and her own predicted IV \(IV_M\). She makes a guess \(G\) as to what Alice’s data could be. She asks the server to encrypt:

The server dutifully encrypts that message using the predicted IV \(IV_M\). It computes:

That ciphertext, \(C_M\), is exactly the ciphertext block Alice would have had if her plaintext block was G. So, depending on what the data is, Mallory has figured out if Alice has a criminal record or not, or perhaps some kind of embarrassing disease, or some other issue that Alice really expected the server to keep secret.

Lessons learned: don’t let IVs be predictable. Also, don’t roll your own cryptosystems. In a secure system, Alice and Mallory’s records probably wouldn’t be encrypted using the same key.

Attacks on CBC mode with the key as the IV

Many CBC systems set the key as the initialization vector. This seems like a good idea: you always need a shared secret key already anyway. It yields a nice performance benefit, because the sender and the receiver don’t have to communicate the IV explicitly, they already know the key (and therefore the IV) ahead of time. Plus, the key is definitely unpredictable because it’s secret: if it were predictable, the attacker could just predict the key directly and already have won. Conveniently, many block ciphers have block sizes that are the same length or less than the key size, so the key is big enough.

This setup is completely insecure. If Alice sends a message to Bob, Mallory, an active adversary who can intercept and modify the message, can perform a chosen ciphertext attack to recover the key.

Alice turns her plaintext message \(P\) into three blocks \(P_1 P_2 P_3\) and encrypts it in CBC mode with the secret key \(k\) and also uses \(k\) as the IV. She gets a three block ciphertext \(C = C_1 C_2 C_3\), which she sends to Bob.

Before the message reaches Bob, Mallory intercepts it. She modifies the message to be \(C^{\prime} = C_1 Z C_1\), where \(Z\) is a block filled with null bytes (value zero).

Bob decrypts \(C^{\prime}\), and gets the three plaintext blocks \(P^{\prime}_1, P^{\prime}_2, P^{\prime}_3\):

\(R\) is some random block. Its value doesn’t matter.

Under the chosen-ciphertext attack assumption, Mallory recovers that decryption. She is only interested in the first block (\(P^{\prime}_1 = P_1\)) and the third block (\(P^{\prime}_3 = P_1 ⊕ IV\)). By XORing those two together, she finds \((P_1 ⊕ IV) ⊕ P_1 = IV\). But, the IV is the key, so Mallory successfully recovered the key by modifying a single message.

Lesson learned: don’t use the key as an IV. Part of the fallacy in the introduction is that it assumed secret data could be used for the IV, because it only had to be unpredictable. That’s not true: “secret” is just a different requirement from “not secret”, not necessarily a stronger one. It is not generally okay to use secret information where it isn’t required, precisely because if it’s not supposed to be secret, the algorithm may very well treat it as non-secret, as is the case here. There are plenty of systems where it is okay to use a secret where it isn’t required. In some cases you might even get a stronger system as a result, but the point is that it is not generally true, and depends on what you’re doing.

CBC bit flipping attacks

An interesting attack on CBC mode is called a bit flipping attack. Using a CBC bit flipping attack, attackers can modify ciphertexts encrypted in CBC mode so that it will have a predictable effect on the plaintext.

This may seem like a very strange definition of “attack” at first. The attacker will not even attempt to decrypt any messages, but they will just be flipping some bits in a plaintext. We will demonstrate that the attacker can turn the ability to flip some bits in the plaintext into the ability to have the plaintext say whatever they want it to say, and, of course, that can lead to very serious problems in real systems.

Suppose we have a CBC encrypted ciphertext. This could be, for example, a cookie. We take a particular ciphertext block, and we flip some bits in it. What happens to the plaintext?

When we “flip some bits”, we do that by XORing with a sequence of bits, which we’ll call \(X\). If the corresponding bit in \(X\) is 1, the bit will be flipped; otherwise, the bit will remain the same.

When we try to decrypt the ciphertext block with the flipped bits, we will get indecipherable⁴ nonsense. Remember how CBC decryption works: the output of the block cipher is XORed with the previous ciphertext block to produce the plaintext block. Now that the input ciphertext block \(C_i\) has been modified, the output of the block cipher will be some random unrelated block, and, statistically speaking, nonsense. After being XORed with that previous ciphertext block, it will still be nonsense. As a result, the produced plaintext block is still just nonsense. In the illustration, this unintelligible plaintext block is \(P_i^{\prime}\).

However, in the block after that, the bits we flipped in the ciphertext will be flipped in the plaintext as well! This is because, in CBC decryption, ciphertext blocks are decrypted by the block cipher, and the result is XORed with the previous ciphertext block. But since we modified the previous ciphertext block by XORing it with \(X\), the plaintext block \(P_{i + 1}\) will also be XORed with \(X\). As a result, the attacker completely controls that plaintext block \(P_{i + 1}\), since they can just flip the bits that aren’t the value they want them to be.

TODO: add previous illustration, but mark the path X takes to influence P prime {i + 1} in red or something

This may not sound like a huge deal at first. If you don’t know the plaintext bytes of that next block, you have no idea which bits to flip in order to get the plaintext you want.

To illustrate how attackers can turn this into a practical attack, let’s consider a website using cookies. When you register, your chosen user name is put into a cookie. The website encrypts the cookie and sends it to your browser. The next time your browser visits the website, it will provide the encrypted cookie; the website decrypts it and knows who you are.

An attacker can often control at least part of the plaintext being encrypted. In this example, the user name is part of the plaintext of the cookie. Of course, the website just lets you provide whatever value for the user name you want at registration, so the attacker can just add a very long string of Z bytes to their user name. The server will happily encrypt such a cookie, giving the attacker an encrypted ciphertext that matches a plaintext with many such Z bytes in them. The plaintext getting modified will then probably be part of that sequence of Z bytes.

An attacker may have some target bytes that they’d like to see in the decrypted plaintext, for example, ;admin=1;. In order to figure out which bytes they should flip (so, the value of \(X\) in the illustration), they just XOR the filler bytes (~ZZZ~…) with that target. Because two XOR operations with the same value cancel each other out, the two filler values (~ZZZ~…) will cancel out, and the attacker can expect to see ;admin=1; pop up in the next plaintext block:

This attack is another demonstration of an important cryptographic principle: encryption is not authentication! It’s virtually never sufficient to simply encrypt a message. It may prevent an attacker from reading it, but that’s often not even necessary for the attacker to be able to modify it to say whatever they want it to. This particular problem would be solved by also securely authenticating the message. We’ll see how you can do that later in the book; for now, just remember that we’re going to need authentication in order to produce secure cryptosystems.

Padding

So far, we’ve conveniently assumed that all messages just happened to fit exactly in our system of block ciphers, be it CBC or ECB. That means that all messages happen to be a multiple of the block size, which, in a typical block cipher such as AES, is 16 bytes. Of course, real messages can be of arbitrary length. We need some scheme to make them fit. That process is called padding.

Padding with zeroes (or some other pad byte)

One way to pad would be to simply append a particular byte value until the plaintext is of the appropriate length. To undo the padding, you just remove those bytes. This scheme has an obvious flaw: you can’t send messages that end in that particular byte value, or you will be unable to distinguish between padding and the actual message.

PKCS#5/PKCS#7 padding

A better, and much more popular scheme, is PKCS#5/PKCS#7 padding.

PKCS#5, PKCS#7 and later CMS padding are all more or less the same idea⁵. Take the number of bytes you have to pad, and pad them with that many times the byte with that value. For example, if the block size is 8 bytes, and the last block has the three bytes 12 34 45, the block becomes 12 34 45 05 05 05 05 05 after padding.

If the plaintext happened to be exactly a multiple of the block size, an entire block of padding is used. Otherwise, the recipient would look at the last byte of the plaintext, treat it as a padding length, and almost certainly conclude the message was improperly padded.

CBC padding attacks

We can refine CBC bit flipping attacks to trick a recipient into decrypting arbitrary messages!

As we’ve just discussed, CBC mode requires padding the message to a multiple of the block size. If the padding is incorrect, the recipient typically rejects the message, saying that the padding was invalid. We can use that tiny bit of information about the padding of the plaintext to iteratively decrypt the entire message.

The attacker will do this, one ciphertext block at a time, by trying to get an entire plaintext block worth of valid padding. We’ll see that this tells them the decryption of their target ciphertext block, under the block cipher. We’ll also see that you can do this efficiently and iteratively, just from that little leak of information about the padding being valid or not.

It may be helpful to keep in mind that a CBC padding attack does not actually attack the padding for a given message; instead the attacker will be constructing paddings to decrypt a message.

To mount this attack, an attacker only needs two things:

1. A target ciphertext to decrypt
2. A padding oracle: a function that takes ciphertexts and tells the attacker if the padding was correct

As with the ECB encryption oracle, the availability of a padding oracle may sound like a very unrealistic assumption. The massive impact of this attack proves otherwise. For a long time, most systems did not even attempt to hide if the padding was valid or not. This attack remained dangerous for a long time after it was originally discovered, because it turns out that in many systems it is extremely difficult to actually hide if padding is valid or not. We will go into this problem in more detail both in this chapter and in later chapters.

In this chapter, we’ll assume that PKCS#5/PKCS#7 padding is being used, since that’s the most popular option. The attack is general enough to work on other kinds of padding, with minor modifications.

Decrypting the first byte

The attacker fills a block with arbitrary bytes \(R = r_1, r_2\ldots r_b\). They also pick a target block \(C_i\) from the ciphertext that they’d like to decrypt. The attacker asks the padding oracle if the plaintext of \(R \| C_i\) has valid padding. Statistically speaking, such a random plaintext probably won’t have valid padding: the odds are in the half-a-percent ballpark. If by pure chance the message happens to already have valid padding, the attacker can simply skip the next step.

Next, the attacker tries to modify the message so that it does have valid padding. They can do that by indirectly modifying the last byte of the plaintext: eventually that byte will be 01, which is always valid padding. In order to modify the last byte of a plaintext block, the attacker modifies the last byte of the previous ciphertext block. This works exactly like it did with CBC bit flipping attacks. That previous ciphertext block is the block \(R\), so the byte being modified is the last byte of \(R\), \(r_b\).

The attacker tries all possible values for that last byte. There are several ways of doing that: modular addition, XORing it with all values up to 256, or even picking randomly; the only thing that matters is that the attacker tries all of them. Eventually, the padding oracle will report that for some ciphertext block \(R\), the decrypted plaintext of \(R \| C_i\) has valid padding.

Discovering the padding length

The oracle has just told the attacker that for our chosen value of \(R\), the plaintext of \(R \| C_i\) has valid padding. Since we’re working with PKCS#5 padding, that means that the plaintext block \(P_i\) ends in one of the following byte sequences:

• 01
• 02 02
• 03 03 03
• …

The first option (01) is much more likely than the others, since it only requires one byte to have a particular value. The attacker is modifying that byte to take every possible value, so it is quite likely that they happened to stumble upon 01. All of the other valid padding options not only require that byte to have some particular value, but also one or more other bytes. For an attacker to be guaranteed a message with a valid 01 padding, they just have to try every possible byte. For an attacker to end up with a message with a valid 02 02 padding, they have to try every possible byte and happen to have picked a combination of \(C\) and \(R\) that causes the plaintext to have a 02 in that second-to-last position. (To rephrase: the second-to-last byte of the decryption of the ciphertext block, XORed with the second-to-last byte of \(R\), is 02.)

In order to successfully decrypt the message, we still need to figure out which one of those options is the actual value of the padding. To do that, we try to discover the length of the padding by modifying bytes starting at the left-hand side of \(P_i\) until the padding becomes invalid again. As with everything else in this attack, we modify those bytes in \(P_i\) by modifying the equivalent bytes in our chosen block \(R\). As soon as padding breaks, you know that the last byte you modified was part of the valid padding, which tells you how many padding bytes there are. Since we’re using PKCS#5 padding, that also tells you what their value is.

Let’s illustrate this with an example. Suppose we’ve successfully found some block \(R\) so that the plaintext of \(R \| C_i\) has valid padding. Let’s say that padding is 03 03 03. Normally, the attacker wouldn’t know this; the point of this procedure is to discover what that padding is. Suppose the block size is 8 bytes. So, we (but not the attacker) know that \(P_i\) is currently:

In that equation, \(p_0 \ldots\) are some bytes of the plaintext. Their actual value doesn’t matter: the only thing that matters is that they’re not part of the padding. When we modify the first byte of \(R\), we’ll cause a change in the first byte of \(P_i\), so that \(p_0\) becomes some other byte \(p^{\prime}_0\):

As you can see, this doesn’t affect the validity of the padding. It also does not affect \(p_1\), \(p_2\), \(p_3\) or \(p_4\). However, when we continue modifying subsequent bytes, we will eventually hit a byte that is part of the padding. For example, let’s say we turn that first 03 into 02 by modifying \(R\). \(P_i\) now looks like this:

Since 02 03 03 isn’t valid PKCS#5 padding, the server will reject the message. At that point, we know that once we modify six bytes, the padding breaks. That means the sixth byte is the first byte of the padding. Since the block is 8 bytes long, we know that the padding consists of the sixth, seventh and eighth bytes. So, the padding is three bytes long, and, in PKCS#5, equal to 03 03 03.

A clever attacker who’s trying to minimize the number of oracle queries can leverage the fact that longer valid padding becomes progressively more rare. They can do this by starting from the penultimate byte instead of the beginning of the block. The advantage to this method is that short paddings (which are more common) are detected more quickly. For example, if the padding is 0x01 and an attacker starts modifying the penultimate byte, they only need one query to learn what the padding was. If the penultimate byte is changed to any other value and the padding is still valid, the padding must be 0x01. If the padding is not valid, the padding must be at least 0x02 0x02. So, they go back to the original block and start modifying the third byte from the back. If that passes, the padding was indeed 0x02 0x02, otherwise the padding must be at least 0x03 0x03 0x03. The process repeats until they’ve found the correct length. This is a little trickier to implement; you can’t just keep modifying the same block (if it’s mutable), and you’re waiting for the oracle to fail instead of pass, which can be confusing. But other than being faster at the cost of being slightly more complex, this technique is equivalent to the one described above.

For the next section, we’ll assume that it was just 01, since that is the most common case. The attack doesn’t really change depending on the length of the padding. If you guess more bytes of padding correctly, that just means that there are fewer remaining bytes you will have to guess manually. (This will become clear once you understand the rest of the attack.)

Decrypting one byte

At this point, the attacker has already successfully decrypted the last byte of the target block of ciphertext! Actually, we’ve decrypted as many bytes as we have valid padding; we’re just assuming the worst case scenario where there is only a single byte. How? The attacker knows that the last byte of the decrypted ciphertext block \(C_i\) (we’ll call that byte \(D(C_i)[b]\)), XORed with the iteratively found value \(r_b\), is 01:

By moving the XOR operation to the other side, the attacker gets:

The attacker has now tricked the receiver into revealing the value of the last byte of the block cipher decryption of \(C_i\).

Decrypting subsequent bytes

Next, the attacker tricks the receiver into decrypting the next byte. Remember the previous equation, where we reasoned that the last byte of the plaintext was 01:

Now, we’d like to get that byte to say 02, to produce an almost valid padding: the last byte would be correct for a 2-byte PKCS#5 padding (02 02), but that second-to-last byte probably isn’t 02 yet. To do that, we XOR with 01 to cancel the 01 that’s already there (since two XORs with the same value cancel each other out), and then we XOR with 02 to get 02:

So, to produce a value of 02 in the final position of the decrypted plaintext, the attacker replaces \(r_b\) with:

This accomplishes the goal of almost valid padding. Then, they try all possible values for the second-to-last byte (index \(b - 1\)). Eventually, one of them will cause the message to have valid padding. Since we modified the random block so that the final byte of the plaintext will be 02, the only byte in the second-to-last position that can cause valid padding is 02 as well. Using the same math as above, the attacker has recovered the second-to-last byte.

Then, it’s just rinse and repeat. The last two bytes are modified to create an almost-valid padding of 03 03, then the third byte from the right is modified until the padding is valid, and so on. Repeating this for all the bytes in the block means the attacker can decrypt the entire block; repeating it for different blocks means the attacker can read the entire message.

This attack has proven to be very subtle and hard to fix. First of all, messages should be authenticated, as well as encrypted. That would cause modified messages to be rejected. However, many systems decrypt (and remove padding) before authenticating the message; so the information about the padding being valid or not has already leaked. We will discuss secure ways of authenticating messages later in the book.

You might consider just getting rid of the “invalid padding” message; declaring the message invalid without specifying why it was invalid. That turns out to only be a partial solution for systems that decrypt before authenticating. Those systems would typically reject messages with an invalid padding slightly faster than messages with a valid padding. After all, they didn’t have to do the authentication step: if the padding is invalid, the message can’t possibly be valid. An attack that leaks secret information through timing differences is called a timing attack, which is a special case of a side-channel attack: attacks on the practical implementation of a cryptosystem rather than its “perfect” abstract representation. We will talk about these kinds of attacks more later in the book.

That discrepancy was commonly exploited as well. By measuring how long it takes the recipient to reject the message, the attacker can tell if the recipient performed the authentication step. That tells them if the padding was correct or not, providing the padding oracle to complete the attack.

The principal lesson learned here is, again, not to design your own cryptosystems. The main way to avoid this particular problem is by performing constant time authentication, and authenticating the ciphertext before decrypting it. We will talk more about this in a later chapter on message authentication.

Native stream ciphers

In addition to block ciphers being used in a particular mode of operation, there are also “native” stream ciphers algorithms that are designed from the ground up to be a stream cipher.

The most common type of stream cipher is called a synchronous stream cipher. These algorithms produce a long stream of pseudorandom bits from a secret symmetric key. This stream, called the keystream, is then XORed with the plaintext to produce the ciphertext. Decryption is the identical operation as encryption, just repeated: the keystream is produced from the key, and is XORed with the ciphertext to produce the plaintext.

You can see how this construction looks quite similar to a one-time pad, except that the truly random one-time pad has been replaced by a pseudorandom stream cipher.

There are also asynchronous or self-synchronizing stream ciphers, where the previously produced ciphertext bits are used to produce the current keystream bit. This has the interesting consequence that a receiver can eventually recover if some ciphertext bits are dropped. This is generally not considered to be a desirable property anymore in modern cryptosystems, which instead prefer to send complete, authenticated messages. As a result, these stream ciphers are very rare, and we don’t talk about them explicitly in this book. Whenever someone says “stream cipher”, it’s safe to assume they mean the synchronous kind.

Historically, native stream ciphers have had their issues. NESSIE, an international competition for new cryptographic primitives, for example, did not result in any new stream ciphers, because all of the participants were broken before the competition ended. RC4, one of the most popular native stream ciphers, has had serious known issues for years. By comparison, some of the constructions using block ciphers seem bulletproof.

Fortunately, more recently, several new cipher algorithms provide new hope that we can get practical, secure and performant stream ciphers.

RC4

By far the most common native stream cipher in common use on desktop and mobile devices is RC4.

RC4 is sometimes also called ARCFOUR or ARC4, which stands for alleged RC4. While its source code has been leaked and its implementation is now well-known, RSA Security (the company that authored RC4 and still holds the RC4 trademark) has never acknowledged that it is the real algorithm.

It quickly became popular because it’s very simple and very fast. It’s not just extremely simple to implement, it’s also extremely simple to apply. Being a synchronous stream cipher, there’s little that can go wrong; with a block cipher, you’d have to worry about things like modes of operation and padding. Clocking in at around 13.9 cycles per byte, it’s comparable to AES-128 in CTR (12.6 cycles per byte) or CBC (16.0 cycles per byte) modes. AES came out a few years after RC4; when RC4 was designed, the state of the art was 3DES, which was excruciatingly slow by comparison (134.5 cycles per byte in CTR mode).

An in-depth look at RC4

On the other hand, RC4 is incredibly simple, and it may be worth skimming this section.

RC4 is, unfortunately, quite broken. To better understand just how broken, we’ll take a look at how RC4 works. The description requires understanding modular addition; if you aren’t familiar with it, you may want to review the tutorial on modular addition

Everything in RC4 revolves around a state array and two indexes into that array. The array consists of 256 bytes forming a permutation: that is, all possible index values occur exactly once as a value in the array. That means it maps every possible byte value to every possible byte value: usually different, but sometimes the same one. We know that it’s a permutation because \(S\) starts as one, and all operations that modify \(S\) always swap values, which obviously keeps it a permutation.

RC4 consists of two major components that work on two indexes \(i, j\) and the state array \(S\):

1. The key scheduling algorithm, which produces an initial state array \(S\) for a given key.
2. The pseudorandom generator, which produces the actual keystream bytes from the state array \(S\) which was produced by the key scheduling algorithm. The pseudorandom generator itself modifies the state array as it produces keystream bytes.

The key scheduling algorithm

The key scheduling algorithm starts with the identity permutation. That means that each byte is mapped to itself.

Then, the key is mixed into the state. This is done by letting index \(i\) iterate over every element of the state. The \(j\) index is found by adding the current value of \(j\) (starting at 0) with the next byte of the key, and the current state element:

Once \(j\) has been found, \(S[i]\) and \(S[j]\) are swapped:

This process is repeated for all the elements of \(S\). If you run out of key bytes, you just wrap around on the key. This explains why RC4 accepts keys from anywhere between 1 and 256 bytes long. Usually, 128 bit (16 byte) keys are used, which means that each byte in the key is used 16 times.

Or, in Python:

from itertools import cycle

def key_schedule(key):
    s = range(256)
    key_bytes = cycle(ord(x) for x in key)

    j = 0
    for i in range(256):
        j = (j + s[i] + next(key_bytes)) % 256
        s[i], s[j] = s[j], s[i]

    return s

The pseudorandom generator

The pseudorandom generator is responsible for producing pseudorandom bytes from the state \(S\). These bytes form the keystream, and are XORed with the plaintext to produce the ciphertext. For each index \(i\), it computes \(j = j + S[i]\) (\(j\) starts at 0). Then, \(S[i]\) and \(S[j]\) are swapped:

To produce the output byte, \(S[i]\) and \(S[j]\) are added together. Their sum is used as an index into \(S\); the value at \(S[S[i] + S[j]]\) is the keystream byte \(K_i\):

We can express this in Python:

def pseudorandom_generator(s):
    j = 0
    for i in cycle(range(256)):
        j = (j + s[i]) % 256
        s[i], s[j] = s[j], s[i]

        k = (s[i] + s[j]) % 256
        yield s[k]

Attacks

The section on the attacks on RC4 is a good deal more complicated than RC4 itself, so you may want to skip this even if you’ve read this far.

There are many attacks on RC4-using cryptosystems where RC4 isn’t really the issue, but are caused by things like key reuse or failing to authenticate the message. We won’t discuss these in this section. Right now, we’re only talking about issues specific to the RC4 algorithm itself.

Intuitively, we can understand how an ideal stream cipher would produce a stream of random bits. After all, if that’s what it did, we’d end up in a situation quite similar to that of a one-time pad.

The stream cipher is ideal if the best way we have to attack it is to try all of the keys, a process called brute-forcing the key. If there’s an easier way, such as through a bias in the output bytes, that’s a flaw of the stream cipher.

Throughout the history of RC4, people have found many such biases. In the mid-nineties, Andrew Roos noticed two such flaws:

• The first three bytes of the key are correlated with the first byte of the keystream.
• The first few bytes of the state are related to the key with a simple (linear) relation.

For an ideal stream cipher, the first byte of the keystream should tell me nothing about the key. In RC4, it gives me some information about the first three bytes of the key. The latter seems less serious: after all, the attacker isn’t supposed to know the state of the cipher.

As always, attacks never get worse. They only get better.

Adi Shamir and Itsik Mantin showed that the second byte produced by the cipher is twice as likely to be zero as it should be. Other researchers showed similar biases in the first few bytes of the keystream. This sparked further research by Mantin, Shamir and Fluhrer, showing large biases in the first bytes of the keystream. fms:rc4 They also showed that knowing even small parts of the key would allow attackers to make strong predictions about the state and outputs of the cipher. Unlike RC4, most modern stream ciphers provide a way to combine a long-term key with a nonce (a number used once), to produce multiple different keystreams from the same long-term key. RC4, by itself, doesn’t do that. The most common approach was also the simplest: concatenate⁶ the long-term key \(k\) with the nonce \(n\): \(k \| n\), taking advantage of RC4’s flexible key length requirements. In this context, concatenation means the bits of \(n\) are appended to the bits of \(k\). This scheme meant attackers could recover parts of the combined key, eventually allowing them to slowly recover the long-term key from a large amount of messages (around \(2^{24}\) to \(2^{26}\), or tens of millions of messages).

WEP, a standard for protecting wireless networks that was popular at the time, was heavily affected by this attack, because it used this simplistic nonce combination scheme. A scheme where the long-term key and the nonce had been securely combined (for example using a key derivation function or a cryptographic hash function) wouldn’t have had this weakness. Many other standards including TLS were therefore not affected.

Again, attacks only get better. Andreas Klein showed more extensive correlation between the key and the keystream. Instead of tens of millions of messages with the Fluhrer, Mantin, Shamir attacks, attackers now only needed several tens of thousands of messages to make the attack practical. This was applied against WEP with great effect.

In 2013, a team of researchers at Royal Holloway in London produced a combination of two independent practical attacks. These attacks proved to be very damning for RC4: while RC4’s weaknesses had been known for a long time, they finally drove the point home for everyone that it really shouldn’t be used anymore.

The first attack is based on single-byte biases in the first 256 bytes of the keystream. By performing statistical analysis on the keystreams produced by a large number of keys, they were able to analyze the already well-known biases in the early keystream bytes of RC4 in much greater detail.

The second attack is based on double byte biases anywhere in the keystream. It turns out that adjacent bytes of the keystream have an exploitable relation, whereas in an ideal stream cipher you would expect them to be completely independent.

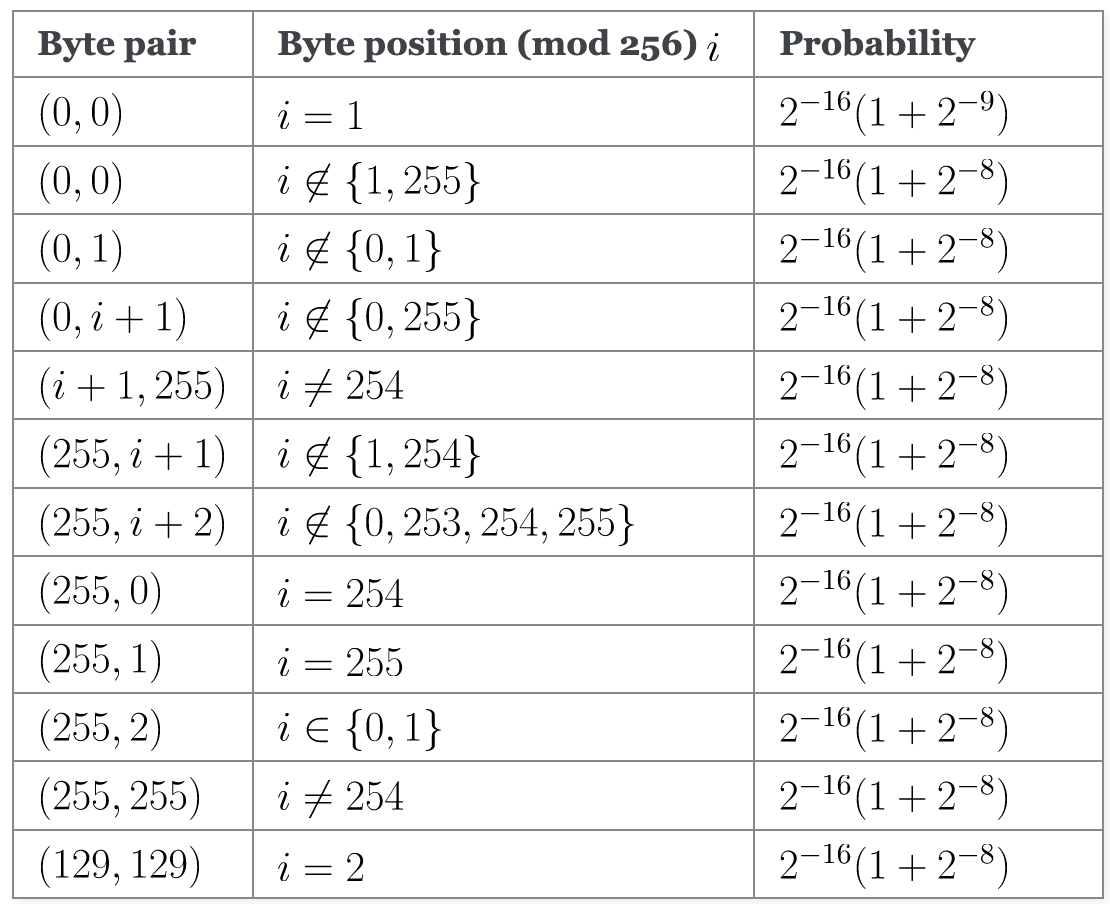
This table may seem a bit daunting at first. The probability expression in the rightmost column may look a bit complex, but there’s a reason it’s expressed that way. Suppose that RC4 was a good stream cipher, and all values occurred with equal probability. Then you’d expect the probability for any given byte value to be \(2^{-8}\) since there are \(2^8\) different byte values. If RC4 was a good stream cipher, two adjacent bytes would each have probability \(2^{-8}\), so any given pair of two bytes would have probability \(2^{-8} \cdot 2^{-8} = 2^{-16}\). However, RC4 isn’t an ideal stream cipher, so these properties aren’t true. By writing the probability in the \(2^{-16} (1 + 2^{-k})\) form, it’s easier to see how much RC4 deviates from what you’d expect from an ideal stream cipher.

So, let’s try to read the first line of the table. It says that when the first byte \(i = 1\) of any 256-byte chunk from the cipher is \(0\), then the byte following it is slightly more likely (\(1 + 2^{-9}\) times as likely, to be exact) to be 0 than for it to be any other number. We can also see that when one of the keystream bytes is \(255\), you can make many predictions about the next byte, depending on where it occurs in the keystream. It’s more likely to be \(0, 1, 2, 255\), or the position in the keystream plus one or two.

Again, attacks only get better. These attacks have primarily focused on the cipher itself, and haven’t been fully optimized for practical attacks on, say, web services. The attacks can be greatly improved with some extra information about the plaintext you’re attempting to recover. For example, HTTP cookies are often base-64 or hex encoded.

There’s no way around it: we need to stop using RC4. Fortunately, we’ve also developed many secure alternatives. The continuing advances in cryptanalysis of RC4 helped contribute to a sense of urgency regarding the improvement of commonly available cryptographic primitives. Throughout 2013 in particular, this led to large improvements in, for example, browser cryptography (we will discuss browser cryptography, notably SSL/TLS, in a later chapter).

Salsa20

Salsa20 is a newer stream cipher designed by Dan Bernstein. Bernstein is well-known for writing a lot of open source (public domain) software, most of which is either directly security related or built with information security very much in mind.

There are two minor variants of Salsa20, called Salsa20/12 and Salsa20/8, which are simply the same algorithm except with 12 and 8 rounds⁷ respectively, down from the original 20. ChaCha is another, orthogonal tweak of the Salsa20 cipher, which tries to increase the amount of diffusion per round while maintaining or improving performance. ChaCha doesn’t have a “20” after it; specific algorithms do have a number after them (ChaCha8, ChaCha12, ChaCha20), which refers to the number of rounds.

Salsa20 and ChaCha are among the state of the art of modern stream ciphers. There are currently no publicly known attacks against Salsa20, ChaCha, nor against any of their recommended reduced-round variants, that break their practical security.

Both cipher families are also pretty fast. For long streams, Salsa20 takes about 4 cycles per byte for the full-round version, about 3 cycles per byte for the 12-round version and about 2 cycles per byte for the 8-round version, on modern Intel processors and modern AMD processors. ChaCha is (on most platforms) slightly faster still. To put that into comparison, that’s more than three times faster than RC4⁸, approximately three times faster than AES-CTR with a 128 bit key at 12.6 cycles per byte, and roughly in the ballpark of AES GCM mode⁹ with specialized hardware instructions.

Salsa20 has two particularly interesting properties. Firstly, it is possible to “jump” to a particular point in the keystream without computing all previous bits. This can be useful, for example, if a large file is encrypted, and you’d like to be able to do random reads in the middle of the file. While many encryption schemes require the entire file to be decrypted, with Salsa20, you can just select the portion you need. Another construction that has this property is a mode of operation called CTR mode, which we’ll talk about later.

This ability to “jump” also means that blocks from Salsa20 can be computed independently of one another, allowing for encryption or decryption to work in parallel, which can increase performance on multi-core CPUs.

Secondly, it is resistant to many side-channel attacks. This is done by ensuring that no key material is ever used to choose between different code paths in the cipher, and that every round is made up of a fixed-number of constant-time operations. The result is that every block is produced with exactly the same number of operations, regardless of what the key is.

Both stream ciphers are based on an ARX design. One benefit of ARX ciphers is that they are intrinsically constant time. There are no secret memory access patterns that might leak information, as with AES. These ciphers also perform well on modern CPU architectures without needing cipher-specific optimizations. They take advantage of generic vector instructions, where the CPU performs related operations on multiple pieces of data in a single instruction. As a result, ChaCha20 performance is competitive with AES on modern Intel CPUs, even though the latter has specialized hardware.

Here is an example ARX operation:

To find the new value of \(x\), first we perform a modular addition (⊞) of \(y\) and \(z\), then we XOR (\(⊕\)) the result with x and finally we rotate left (\(\lll\)) by \(n\) bits. This is the core round primitive of Salsa20.

Native stream ciphers versus modes of operation

Some texts only consider native stream ciphers to be stream ciphers. This book emphasizes what the functionality of the algorithm is. Since both block ciphers in a mode of operation and a native stream cipher take a secret key and can be used to encrypt a stream, and the two can usually replace each other in a cryptosystem, we just call both of them stream ciphers and are done with it.

We will further emphasize the tight link between the two with CTR mode, a mode of operation which produces a synchronous stream cipher. While there are also modes of operation (like OFB and CFB) that can produce self-synchronizing stream ciphers, these are far less common, and not discussed here.

CTR mode

CTR mode, short for counter mode, is a mode of operation that works by concatenating a nonce with a counter. The counter is incremented with each block, and padded with zeroes so that the whole is as long as the block size. The resulting concatenated string is run through a block cipher. The outputs of the block cipher are then used as the keystream.

![CTR mode: a single nonce \(N\) with a zero-padded counter \(i\) is encrypted by the block cipher to produce a keystream block; this block is XORed with the plaintext block \(P_i\) to produce the ciphertext block \(C_i\).]

This illustration shows a single input block \(N \| 00 \ldots \| i\), consisting of nonce \(N\), current counter value \(i\) and padding, being encrypted by the block cipher \(E\) using key \(k\) to produce keystream block \(S_i\), which is then XORed with the plaintext block \(P_i\) to produce ciphertext block \(C_i\).

Obviously, to decrypt, you do the exact same thing again, since XORing a bit with the same value twice always produces the original bit: \(p_i ⊕ s_i ⊕ s_i = p_i\). As a consequence, CTR encryption and decryption is the same thing: in both cases you produce the keystream, and you XOR either the plaintext or the ciphertext with it in order to get the other one.

For CTR mode to be secure, it is critical that nonces aren’t reused. If they are, the entire keystream will be repeated, allowing an attacker to mount multi-time pad attacks.

This is different from an initialization vector such as the one used by CBC. An IV has to be unpredictable. An attacker being able to predict a CTR nonce doesn’t really matter: without the secret key, they have no idea what the output of the block cipher (the sequence in the keystream) would be.

Like Salsa20, CTR mode has the interesting property that you can jump to any point in the keystream easily: just increment the counter to that point. The Salsa20 paragraph on this topic explains why that might be useful.

Another interesting property is that since any keystream block can be computed completely separately from any other keystream block, both encryption and decryption are very easy to compute in parallel.

Stream cipher bit flipping attacks

Synchronous stream ciphers, such as native stream ciphers or a block cipher in CTR mode, are also vulnerable to a bit flipping attack. It’s similar to CBC bit flipping attacks in the sense that an attacker flips several bits in the ciphertext, and that causes some bits to be flipped in the plaintext.

This attack is actually much simpler to perform on stream ciphers than it is on CBC mode. First of all, a flipped bit in the ciphertext results in the same bit being flipped in the plaintext, not the corresponding bit in the following block. Additionally, it only affects that bit; in CBC bit flipping attacks, the plaintext of the modified block is scrambled. Finally, since the attacker is modifying a sequence of bytes and not a sequence of blocks, the attacks are not limited by the specific block size. In CBC bit flipping attacks, for example, an attacker can adjust a single block, but can’t adjust the adjacent block.

This is yet another example of why authentication has to go hand in hand with encryption. If the message is properly authenticated, the recipient can simply reject the modified messages, and the attack is foiled.

Authenticating modes of operation

There are other modes of operation that provide authentication as well as encryption at the same time. Since we haven’t discussed authentication at all yet, we’ll handle these later.

Remaining problems

We now have tools that will encrypt large streams of data using a small key. However, we haven’t actually discussed how we’re going to agree on that key. As noted in a previous chapter, to communicate between \(n\) people, we need \(\frac{n(n-1)}{2}\) key exchanges. The number of key exchanges grows about as fast as the number of people squared. While the key to be exchanged is a lot smaller now than it was with one-time pads, the fundamental problem of the impossibly large number of key exchanges hasn’t been solved yet. We will tackle that problem in the next section, where we’ll look at key exchange protocols: protocols that allow us to agree on a secret key over an insecure medium.

Additionally, we’ve seen that encryption isn’t enough to provide security: without authentication, it’s easy for attackers to modify the message, and in many flawed systems even decrypt messages. In a future chapter, we’ll discuss how to authenticate messages, to prevent attackers from modifying them.