Books / Patterns for Beginning Programmers / Chapter 20
Conformal Arrays
In many situations there are multiple pieces of data that need to be organized in a way that makes them easy to work with. While this problem can sometimes be solved with a single array, many other times a more powerful organizational scheme is needed. This is where conformal arrays come in.
In this chapter
Motivation
The Federal Reserve Bank tracks monthly data about many aspects of the economy. Suppose you are working with a group that has developed a categorical measure of consumer confidence. The group wants to explore the relationships between its measure of consumer confidence, the consumer price index (CPI), the civilian unemployment rate (in percent), and the M2 money stock (in billions of dollars) for the year 2018 (on a monthly basis). You need to organize this information in such a way that it can be used to conduct a variety of different analyses.
Review
As you know, arrays make it very easy to perform the same operation(s)
on homogeneous values. So, if you were only interested in the CPI, for
example, you could store it in a double[] with twelve elements (since
there are twelve months in the year 2018). Such an array is referred to
as a time series because the index is a measure of time.
However, you need to organize more than just the CPI. You need to organize all 48 data points (12 months of data for 4 different time series) and 12 associated labels (the three-letter abbreviations for the months). Since the elements aren’t homogeneous (i.e., some are numbers and some are three-letter abbreviations), you can’t use a single array.
Thinking About The Problem
Conceptually, the data in this example can be thought of as a table. In fact, time series data (like the data in this example) are often presented in tabular form, as illustrated in Table 17.1. In this case, the table has one column for each type of data and one row for each month.
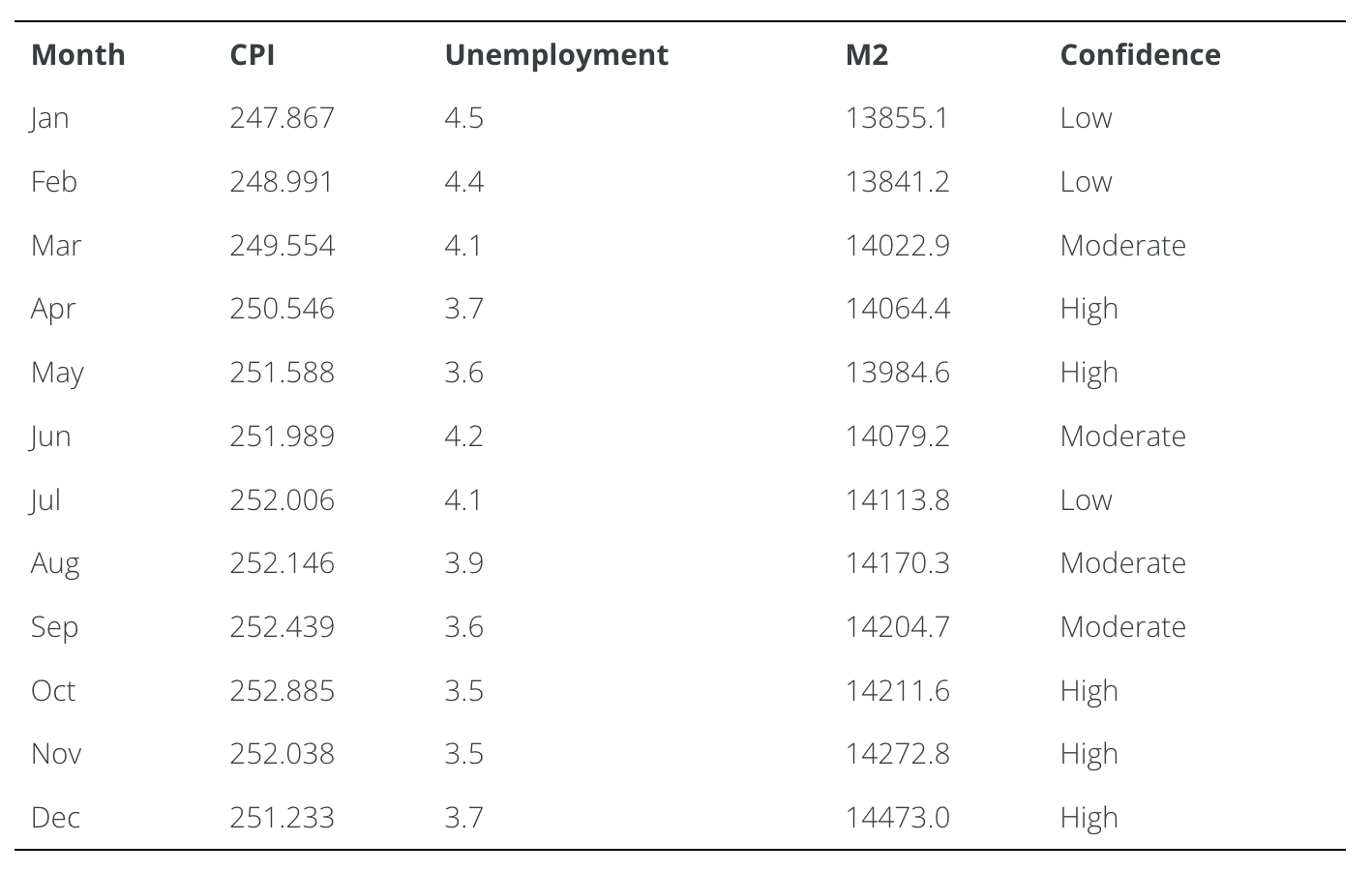
Table 17.1. U.S. Macroeconomic Data for 2018 (Not Seasonally Adjusted)
While there are a variety of different ways of organizing tabular data, none of them are available to you at the moment. Fortunately, you can use multiple different arrays. Doing so just requires a little thought.
A table can be conceptualized in two ways. On the one hand, you can think about a table as consisting of rows, each of which consists of columns. The is called row-major form (i.e., rows first). On the other hand, you can think think about a table as consisting of columns, each of which consists of rows. This is called column-major form. In the first case, one array can be used to store each row; in the second case, one array can be used to store each column
Regardless of which approach you use, the arrays will be conformal. That is, they will share a common index. If you use one array for each column then the common index will be the conceptual row headers. In the example above, if you use this approach, the indexes will correspond to the months. On the other hand, if you use one array for each row then the common index will be the column headers. In the example above, if you use this approach, the indexes will correspond to “Month”, “CPI”, “Unemployment”, “M2”, and “Confidence”.
The Pattern
To obtain a solution to the problem you need only decide whether to use an array for each column or an array for each row. Fortunately, in most situations, this is an easy decision to make. Specifically, you should choose the alternative that satisfies the following criteria:
- The elements of the array must be of the same type; and
- The indexes must be easily representable as
intvalues.
In many situations, only one alternative will satisfy both criteria.
Each such conformal array can then be thought of as an individual
field in a record that has an index number. So, if you have two
arrays named fieldA and fieldB, then record number i consists of
fieldA[i] and fieldB[i]. This is illustrated in Figure
17.1 for some data about four different people.
The names of the people are stored in the String[] named fieldA, and
the number of science fiction books they own are stored in the int[]
named fieldB.

Figure 17.1. An Illustration of Conformal Arrays
Examples
Continuing with the economic example above, its useful to consider both possible approaches for the tabular representation in Table 17.1.
If you were to use one array for each row then the first and last
elements would need to be String objects and the middle three elements
would need to be double values. Hence, this approach doesn’t satisfy
the first criterion and can be eliminated.
If you were to use one array for each column, then all of the elements
of the first and last columns would be String objects and all of the
elements of the three middle columns would be double values. Hence,
the first criterion is satisfied. In addition, the second criterion is
satisfied because you can use a 0-based int representation of the
months (i.e., 0 for January, 1 for February, etc.).
This leads to the following conformal arrays:
// Month of the year
String[] month = {
"Jan", "Feb", "Mar", "Apr", "May", "Jun",
"Jul", "Aug", "Sep", "Oct", "Nov", "Dec" };
// Consumer price index for all urban consumers
// (not seasonally adjusted)
double[] cpiaucns = {
247.867, 248.991, 249.554, 250.546, 251.588, 251.989,
252.006, 252.146, 252.439, 252.885, 252.038, 251.233 };
// Unemployment rate (not seasonally adjusted)
double[] unratensa = {
4.5, 4.4, 4.1, 3.7, 3.6, 4.2,
4.1, 3.9, 3.6, 3.5, 3.5, 3.7 };
// M2 money stock (not seasonally adjusted)
double[] m2ns = {
13855.1, 13841.2, 14022.9, 14064.4, 13984.6, 14079.2,
14113.8, 14170.3, 14204.7, 14211.6, 14272.8, 14473.0 };
// Consumer confidence
String[] confidence = {
"Low", "Low", "Moderate", "High", "High", "Moderate",
"Low", "Moderate", "Moderate", "High", "High", "High" };
Then, if you want to work with the CPI and M2 for May (month 4 in a
0-based numbering scheme), you simply need to use cpiaucns[4] and
m2ns[4]. The corresponding abbreviation would then be month[4] and
the corresponding consumer confidence would be confidence[4].
A Warning
You might be tempted to use conformal arrays for solving the interval
membership problem discussed in Chapter
19.
That is, you might be tempted to create two arrays, left and right,
that contain the left and right bounds for each interval. The
shortcoming of this approach is that it is error-prone. In particular,
observe that there is a very important constraint that involves
right[i] and left[i+1] for element i (e.g., the two must be equal
or differ by one, depending on exactly how they are used), and it is
easy to inadvertently violate this constraint. Hence, unless there are
gaps in the intervals, it is better to use a single array as described
in Chapter
19.
Looking Ahead
It is often necessary to look-up information using a non-numeric key. How to do this efficiently is a topic for a course on data structures and algorithms. However, ignoring efficiency, conformal arrays are part of the answer.
To see how, consider the example above. Though it isn’t necessary to do
so, because you know how the months correspond to indexes in the other
arrays, you could use the month array to find the index that
corresponds to a particular month. In particular, consider the following
method:
public static int find(String needle, String[] haystack) {
int i, n;
i = 0;
n = haystack.length;
while (i < n) {
if (needle.equals(haystack[i])) {
return i;
}
++i;
}
return -1;
}
It returns the index of the element in haystack that equals the
needle. You could then use this method to get the CPI and M2 for May
as follows:
int i;
i = find("May", month);
// Do something with cpiaucns[i] and m2ns[i]
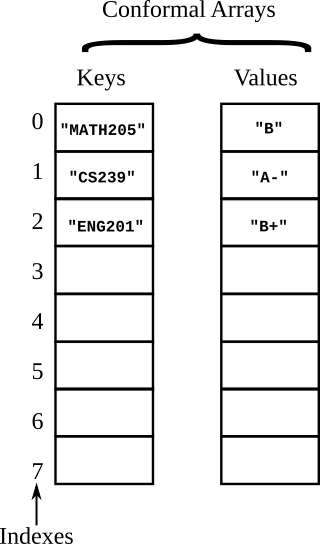
Figure 17.2. An Example of Keys and Values in Conformal Arrays
As another (more relevant) example, suppose you have conformal arrays that are holding course identifiers and the corresponding grades in those courses as in Figure 17.2. You could get the grade for a particular course using the following method:
public static String getGrade(String key,
String[] courses, String[] grades) {
int i, n;
n = courses.length;
i = 0;
while (i < n) {
if (key.equals(courses[i])) {
return grades[i];
}
++i;
}
return "NA";
}



