Books / Patterns for Beginning Programmers / Chapter 5
Arithmetic on the Circle
When children are first taught to count, they are introduced to the concept of a number line. That approach then subconsciously influences the way people think about arithmetic throughout their lives. However, one can also perform arithmetic on a number circle, which turns out to be a good way to solve an enormous number of programming problems.
Motivation
Quite frequently, values can be increased without bound. For example, if you start with $3.00 and someone keeps giving you dollar bills, you will have more and more dollar bills (subject, of course, to tax laws and the like). However, in some cases, values don’t keep increasing, they “repeat” (for lack of a better word). For example, if you start at three o’clock (i.e., 3:00) and keep increasing the hour of the day, you will (in fairly short order) get back to three o’clock (ignoring the AM/PM distinction, for the moment). To handle these kinds of situations you need to re-think addition and subtraction.
Review
A number line is usually represented as a line with arrow heads at both ends (indicating that it continues forever in both directions) and labeled tick marks (indicating the integers). A traditional number line increases to the right and decreases to the left. An example, focusing on the first twelve non-negative integers, is illustrated in Figure 4.1.

Figure 4.1. The Traditional Number Line
Addition on the number line involves moving to the right from a particular tick mark. So, for example, suppose you are interested in the quantity \(x + 2\). Then, you locate \(x\) on the number line and move \(2\) tick marks to the right. This is illustrated in Figure 4.2.

Figure 4.2. Addition on a Line
Similarly, subtraction on the number line involves moving to the left from a particular tick mark. So, for example, suppose you are interested in the quantity \(x - 1\). Then, you locate \(x\) on the number line and move \(1\) tick mark to the left. This is illustrated in Figure 4.3.

Figure 4.3. Subtraction on a Line
So, if you start with $3.00 and someone gives you fifteen more dollars, you will have $18.00. On the other hand, if you start with $3.00 and spend $5.00, you will have $-2.00 (i.e., you will be $2.00 in debt). Does this sound like elementary school? Good, it should.
Thinking About The Problem
Now, however, consider what happens if you start at three o’clock (i.e., 3:00) and add fifteen hours. You don’t wind up at eighteen o’clock (i.e., 18:00) because there is no such hour (on a traditional twelve-hour clock). Instead, what happens conceptually is that the hour “circles around”. Indeed, on a traditional analog clock, this is what happens physically, as well. It also provides a way of thinking about the problem — use a number circle instead of a number line.
A number circle is a circle with labeled tick marks (indicating the integers) rather than a line with tick marks. A traditional number circle increases in the clockwise direction and decreases in the counterclockwise direction. An example, which includes the first twelve non-negative integers, is illustrated in Figure 4.4.

Figure 4.4. Numbers on a Circle
Addition on the number circle involves moving in the clockwise direction from a particular tick mark. So, for example, suppose you are interested in the quantity \(x + 2\). Then, you locate \(x\) on the number circle and move \(2\) tick marks in the clockwise direction. This is illustrated in Figure 4.5a.
Similarly, subtraction on the number circle involves moving in the counterclockwise direction from a particular tick mark. So, for example, suppose you are interested in the quantity \(x - 1\). Then, you locate \(x\) on the number circle and move \(1\) tick mark in the counterclockwise direction. This is illustrated in Figure 4.5b.
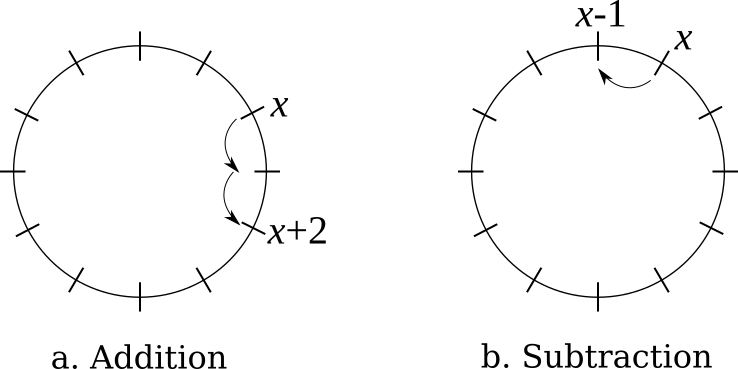
Figure 4.5. Addition and Subtraction on a Circle
The important difference between addition/subtraction on the number line and on the number circle should be readily apparent. On the number line the values are unbounded and never repeat, while on the number circle the values are bounded and (eventually) repeat.
The Pattern
The way to approach problems of this kind is to distinguish the number of times you move around the circle (which you typically aren’t interested in) from where you are on the circle (which you are interested in). Specifically, the pattern works as follows:
-
Use a 0-based set of consecutive integer values.
-
Use integer arithmetic and the following variables:
int cardinality, change, current, passes, remainder; -
If needed, calculate the number of times 0 is passed as follows:
passes = (current + change) / cardinality; -
Calculate the
remainderas follows:remainder = (current + change) % cardinality;
where current denotes the current value, change denotes the change
(either positive or negative), and cardinality denotes the number of
elements in the set of values.
Examples
The arithmetic on the circle pattern arises in a wide variety of situations, some obvious and some less obvious.
Some Obvious Examples
The most obvious example in which arithmetic is performed on a circle is the circular, analog clock (which even looks like a number circle). Indeed, this is exactly the number circle in Figure 4.4, except that noon and midnight are represented as 0 instead of 12. To avoid both this potential source of confusion and the AM/PM issue, consider, instead, a clock that uses military time. In such a clock, midnight is “0 hundred hours”, eleven in the morning is “11 hundred hours”, five in the evening is “17 hundred hours”, etc. Such a clock is illustrated in Figure 4.6.

Figure 4.6. An Analog Military Clock
Some questions involving such a clock are easy to answer. For example, suppose it is currently 5 hundred hours, what time will it be in 8 hours? This doesn’t require any thought; you can use traditional addition to determine that the answer is 13 hundred hours. However, some are more difficult. For example, suppose it is currently 17 hundred hours, what time will it be in 12 hours? Unfortunately, traditional addition is no longer enough to solve this problem. Obviously, the answer isn’t 29 hundred hours, because there is no such time. Instead, you have to account for the fact that you’ve advanced a day. Even worse, suppose it is 17 hundred hours and you want to know the time 93 hours from now. Then, you have to account for the fact that you have advanced several days.
Using the arithmetic on the circle pattern, 17 hundred hours plus 12
hours can be thought of (using integer arithmetic) as a passes of
((17 + 12) / 24) or 29 / 24 or 1 (i.e., one time around the
circle), with a remainder of ((17 + 24) % 24) or 29 % 24 or 5
(i.e., five additional ticks). Similarly, for 17 hundred hours plus 93
hours:
remainder = (17 + 93) % 24;
which is 110 % 24 or 14.
As another example, consider weights. In the United States, weights are
measured in pounds and ounces, and the ounces are constrained to be in
the half-open interval \(\[0, 16)\). So, if you have 9
ounces of gold, and someone gives you 14 ounces of gold, you don’t
normally say that you have 23 ounces of gold, instead you say that you
have 1 pound and 7 ounces of gold. In other words, the value of
current is 9, the value of change is 14, the value of
cardinality is 16 and:
passes = (9 + 14) / 16;
remainder = (9 + 14) % 16;
which means passes is 23 / 16 or 1 pound, and remainder is
23 % 16 or 7 ounces.
Less Obvious Examples
As shown above, arithmetic on the circle can be used with values that are naturally numeric, but they can also be used with categories. One common application is to determine the day of the week some number of days in the future. The set of days of the week (i.e., Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, and Saturday) has a cardinality of
- Using a 0-based numbering scheme, you can denote Sunday by 0, Monday by 1, etc. Then, if it is currently Wednesday (i.e., day of the week 3), you can determine the day of the week 6 days in the future as:
remainder = (3 + 6) % 7;
which is 9 % 7 or 2 (i.e., Tuesday). Similarly, the day of the week
516 days in the future is:
remainder = (3 + 516) % 7;
which is 519 % 7 or 1 (i.e., Monday). Obviously, the same thing can
be done for months of the year. This set has a cardinality of 12 and a
0-based numbering scheme would assign 0 to January, 1 to February, etc.
Less obviously, perhaps, this pattern can be used for categories that
are not normally numbered. For example, suppose you want to know whether
a number is even or odd (a set with cardinality of two). Letting 0
denote the even numbers and 1 denote the odd numbers, you can determine
whether the sum of two numbers, current and change, is even or odd
using:
remainder = (current + change) % 2;
Further, since change can be zero, you can determine whether the
number current is even or odd using:
remainder = current % 2;
which makes sense since a number is even if it is divisible by two with no remainder (sometimes called “evenly divisible by two”).
This pattern can also be used for such things as determining which player’s turn it is in a game, how to cycle through a fixed set of colors in a drawing program, etc. Indeed, this pattern arises so frequently that it is virtually indispensable.



