Books / Patterns for Beginning Programmers / Chapter 26
Centering
Many applications need to center content (of some kind) inside a container (of some kind). Though the content and the containers can vary dramatically, the pattern used to do the centering is very consistent.
Motivation
Suppose you have some text that you need to display on the console, centered on the line containing it. Since the console (typically) uses a fixed-width font, the width of every character (measured in pixels) is the same. As a result, both the width of the text and the width of the line can be measured in characters. Your objective, then, is to determine the column of the line that should contain the first character of the text.
Review
The text in this example is going to be represented as a String
object. So, you can use its length() method to determine the number of
characters in it. Unfortunately, you have no way of specifying the
column of the display to print to when writing to the console. Hence,
you have to create or output a String that is padded on the left with
the appropriate number of spaces, which you can do using an accumulator
(see Chapter
16).
The only problem that remains, then, is the determination of the
appropriate number of spaces.
Thinking About The Problem
Suppose that the line is nine characters wide and 0-based (i.e., the
first character is at position 0). Then, you know that the middle
character in the line has index 4 (i.e., 9 / 2, using integer
division), since there are four characters to the left of index 4 and
four characters to the right of index 4.
Suppose further that the text is five characters wide and is also
0-based. Then, you know that the middle character of the text has index
2 (i.e., 5 / 2), since there are two characters to the left of index
2 and two characters to the right of index 2.
So, in order to center the text in the line, you want character 2 of
the text to be at position 4 of the line. This means that character
0 of the text must be at position 2 of the line.
The Pattern
The centering pattern is nothing more than a generalization of this example. First, instead of text, you should think more generally about content. Second, instead of a line, you should think more generally about a container. Both the content and the container have an extent that generalizes the notion of the width in the example, and a reference that generalizes the notion of a starting character.
The centering problem is to find the reference for the content, given the reference and extent of the container and the extent of the content. Letting \(C\) denote the container, \(c\) denote the content, and the superscripts \(R\), \(E\) and \(M\) denote the reference, extent, and midpoint respectively (for each dimension), the centering pattern involves three steps.
First, you need to calculate the midpoint of the container (which had a reference of 0 and an extent of 9 in the example). You can do this as follows:
\[C^{M}=C^{R}+\left(C^{E} / 2\right)\]Next, you need to calculate the midpoint of the content (which had a width of 5 in the example). You can do this as follows:
\[c^{M}=\left(c^{E} / 2\right)\]Finally, you need to calculate the reference for the content by subtracting the midpoint of the content from the midpoint of the container. That is:
\[c^{R}=C^{M}-c^{M}\]In one dimension (i.e., when the references and the extents can be represented by a single number) as in the text example, this algorithm can be implemented as follows:
public static double center(double containerReference,
double containerExtent,
double contentExtent) {
double containerMidpoint = containerReference + containerExtent / 2.0;
double contentMidpoint = contentExtent / 2.0;
double contentReference = containerMidpoint - contentMidpoint;
return contentReference;
}
Of course, many problems are not one dimensional. For example, images and windows have both a width and a height, and their positions are specified with both a horizontal and a vertical coordinate. Fortunately, the logic is exactly the same for all of the dimensions. Hence, if both the extents and the references are represented as conformal arrays (see Chapter 20), then you can perform the calculations for each dimension independently in the body of a loop as follows:
public static double[] center(double[] containerReference,
double[] containerExtent,
double[] contentExtent) {
int n = containerReference.length;
double[] contentReference = new double[n];
for (int i = 0; i < n; ++i) {
double containerMidpoint = containerReference[i]
+ containerExtent[i] / 2.0;
double contentMidpoint = contentExtent[i] / 2.0;
contentReference[i] = containerMidpoint - contentMidpoint;
}
return contentReference;
}
Examples
Unlike the other patterns in this book, for this pattern it is useful to consider some examples that don’t involve the use of any code.
A One-Dimensional Example
An example of centering in one dimension is illustrated in Figure 21.1. The upright numbers in this figure are the inputs, and the italicized numbers in this figure are the calculated values. This example might, again, involve centering text, but the objective now is to center the text within a portion of a line (e.g., a field with a given width). In this example, the content (i.e., the text) has a width of \(4\), and the field has a width of \(17\) and starts in column \(8\).
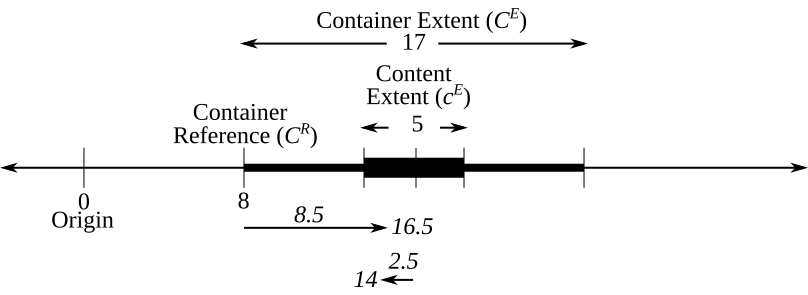
Figure 21.1. Centering in One Dimension
You should begin with the container’s reference and the container’s extent, and use them to calculate the container’s midpoint as follows:
\[\begin{aligned} C^{M} &=C^{R}+\left(C^{E} / 2\right) \\ &=8+(17 / 2) \\ &=8+8.5 \\ &=16.5 \end{aligned}\]In other words, it’s necessary to move \(8.5\) units to the right of the container’s reference of \(8\) to get the container’s midpoint of \(16.5\).
Then, you can calculate the content’s reference as follows:
\[\begin{aligned} c^{R} &=C^{M}-\left(c^{E} / 2\right) \\ &=16.5-(5 / 2) \\ &=16.5-2.5 \\ &=14 \end{aligned}\]In other words, it’s necessary to move \(2.5\) units (half of the content’s width) to the left of the container’s midpoint to get the content’s reference.
A Two-Dimensional Example
An example of centering in two dimensions is illustrated in Figure 21.2. Again, the upright numbers are the inputs, while the numbers in italics are calculated. This example might involve centering an image inside of a window in a graphical user interface (GUI). In this context, the content (i.e., the image) has a width of \(6\) and a height of \(8\) (i.e., is \(6 \times 8\)), and the container (i.e., the window) has a width of \(30\) and a height of \(12\) (i.e., is \(30 \times 12\)).
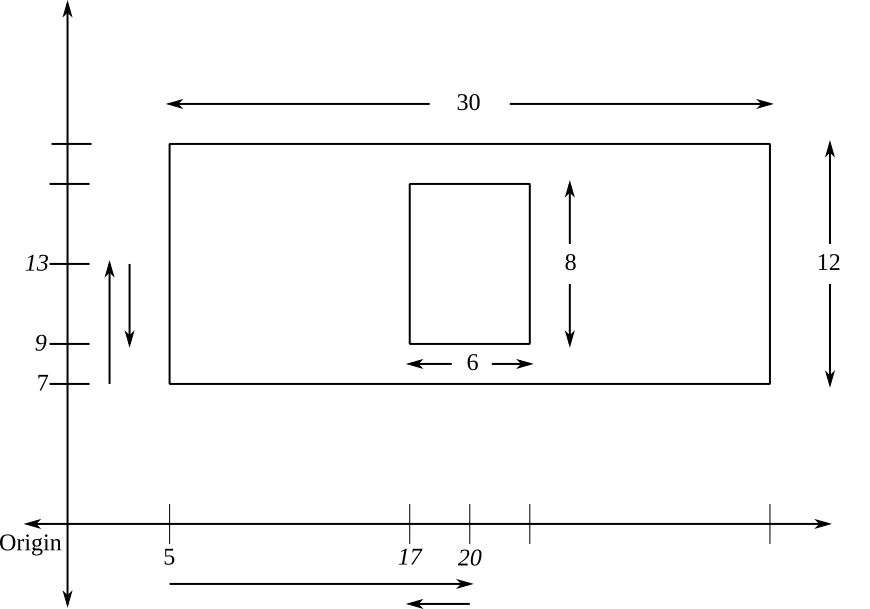
Figure 21.2. Centering in Two Dimensions
Some Warnings
The pattern above can be used in a wide variety of situations, but there are some things that you should be aware of.
Coordinate Systems
All of the figures and examples in this chapter use Euclidean coordinates in which the horizontal coordinates increase from left to right, and the vertical coordinates increase from bottom to top. However, computer graphics tend to use screen coordinates in which the horizontal coordinates increase from left to right but the vertical coordinates increase from top to bottom. This means that the sign of the adjustments in the vertical dimension must be negated.
Using Integers
The code above assumes that the references and extents are all double
values. However, the text example uses int values (since the content
must be an integer and the column positions are integers). Fortunately,
with a little care, the pattern can be used for both int values and
double values.
The first thing to realize is that, if either of the extents is even, then the content can’t be perfectly centered. The calculated integer midpoint will either “lean” to the left or the right of the conceptual real-valued center.
The second thing to realize is the impact of integer division and how it
differs depending on whether the extent is odd or even. To get started
thinking about this issue, just use the pattern exactly as it is
implemented above, replacing the double values with int values, and
consider the container and the content individually.
When the extent of the container is odd, the calculated midpoint
will be at the conceptual center. For example, when the extent is 9 as
in the text example above, the midpoint is 9 / 2 or 4, which leaves
4 characters to the left (i.e., indexes 0, 1, 2, and 3) and 4
characters to the right (i.e., indexes 5, 6, 7, and 8). On the
other hand, when the extent of the container is even, the calculated
midpoint will “lean” right. For example, when the extent is 8, the
midpoint is 8 / 2 or 4, which leaves 4 characters to the left (i.e.,
indexes 0, 1, 2, and 3) but only 3 characters to the right
(i.e., indexes 5, 6, 7).
When the extent of the content is odd, the calculated midpoint will
again be at the conceptual center. For example, when the extent is 5
as in the text example above, the midpoint is 5 / 2 or 2, which
leaves 2 characters to the left (i.e., indexes 0 and 1) and 2
characters to the right (i.e., indexes 3 and 4). So, the leftward
adjustment will be 2 characters. On the other hand, when the extent of
the content is even, the calculated midpoint will again “lean” right.
For example, when the extent is 4, the midpoint is 4 / 2 or 2,
which leaves 2 characters to the left (i.e., indexes 0 and 1) but
only 1 characters to the right (i.e., index 3). So, the leftward
adjustment will still be 2 characters.
Putting all of this together, leads to the following conclusions:
- When the container has an extent of
9, the reference of the content will be4 - 2or2whether the content has an extent of5or4. Hence, when the content has an extent of5it will be exactly centered, and when the content has an extent of4it will “lean” to the left by one character. - When the container has an extent of
8, the reference of the content will be4 - 2or2whether the content has an extent of5or4. Hence, when the content has an extent of5it will “lean” to the right by one character, and when the content has an extent of4it will be exactly centered.
In other words, the “lean” will be at most one character (which is as small as it can be).
Of course, if you want the “lean” to be consistently in one direction or the other, then you can adjust the algorithm slightly depending on whether the extents are odd or even. Fortunately, you can easily identify these cases using the arithmetic on the circle pattern discussed in Chapter 5.
Clipping
The examples in this chapter assume that the container is large enough (in all dimensions) to hold the content. When this is not the case, the content may need to be clipped to fit in the container. Fortunately, the logic for doing so is straightforward.



