Books / Patterns for Beginning Programmers / Chapter 4
Digit Manipulation
In most programming languages, integer types (e.g., int in Java) are
atomic. That is, they do not have constituent parts. However, there
are many situations in which one needs to manipulate the individual
digits of an integer value. This chapter considers different ways of
doing so.
Motivation
Suppose you are writing a program for a credit card company that has accounts of various kinds. All account numbers are nine digits long, they never start with a 0, the left-most three digits represent the issuing bank, and the right-most digit indicates the type of account (e.g., debit, credit, crypto currency).
Because account numbers are nine digits long, and the maximum int
value is \(2^{31}-1\) (or
2,147,483,647), you decide to represent each account
number as an int. However, you realize that this means that you will
need to extract digits from the account number, both from the left and
from the right. In other words, you need to solve some digit
manipulation problems.
Review
Recall that in a decimal (i.e., base 10) representation of a number, each digit is multiplied by a power of 10. The right-most digit is multiplied by \(10^0\) (i.e., 1, and hence is often called the “ones place”), the second digit from the right is multiplied by \(10^1\) (i.e., 10, and hence is often called the “tens place”), and, in general, the digit in position \(n\) (counting from the right, starting at 0) This is illustrated in Figure 3.1. is multiplied by \(10^n\).
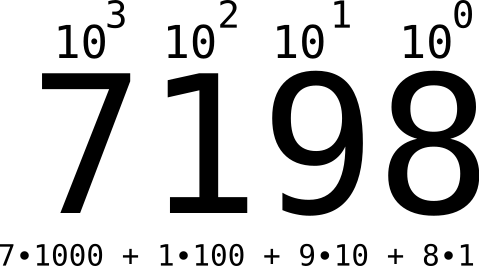
Figure 3.1. Decimal Representation of an Integer
Thinking About The Problem
Since each digit in a base 10 representation of an int corresponds to
a power of 10, you should now be thinking, at least at an intuitive
level, that solutions to digit manipulation problems will involve the
powers of 10. The other thing that should be clear, again at an
intuitive level, is that solutions to the digit manipulation problem
will involve one or more of the arithmetic operations that can be
performed on int values.
You can rule out addition and multiplication almost immediately, since both operations make the number larger. Subtraction might work, but it doesn’t get you very far. Suppose, for example, you wanted to get the right-most digit of \(7198\). You’d need to subtract \(7190\), which requires knowledge of the three left-most digits (multiplied by \(10\)). Similarly, to get the left-most digit, you’d need to subtract \(198\), the three right-most digits, and then divide by \(1000\). The two operations left to consider are integer division and the remainder after integer division.
If you divide \(7198\) by \(10\) (using integer division) you are left with \(719\). In other words, you have dropped the right-most digit and/or extracted the left-most three digits. Similarly, if you divide \(7198\) by \(100\) you are left with \(71\). In other words, you have dropped the right-most two digits and/or extracted the left-most two digits. This is clearly progress.
You can also make progress with the remainder after integer division. If you divide \(7198\) by \(10\), the remainder is \(8\). In other words, you have dropped the left-most three digits and/or extracted the right-most digit. Similarly, if you divide \(7198\) by \(100\), the remainder is \(98\). That is, you have dropped the left-most two digits and/or extracted the right-most two digits.
The Pattern
One aspect of the pattern should now be relatively easy to see, the operation. To drop from the right or extract from the left you must use integer division. On the other hand, to extract from the right or drop from the left you must use the remainder after integer division.
The simpler cases involve counting from the right, and can be handled as follows:
- To drop the \(n\) right-most digits from a number you must divide by \(10^n\).
- To extract the \(n\) right-most digits from a number you must find the remainder after dividing by \(10^n\).
Extracting digits on the left and dropping digits on the left are both slightly more complicated because these operations require knowledge of the number of digits in the number as well as the number of digits to extract or drop. Letting \(N\) denote the number of digits in the number, the pattern can be completed as follows:
- To extract the \(n\) left-most digits from a number you must divide by \(10^{N-n}\).
- To drop the \(n\) left-most digits from a number you must find the remainder after dividing by \(10^{N-n}\).
Examples
Returning to the credit card example, suppose the account number is \(412831758\). To extract the card type from the account number you need to extract the right-most digit. This means that you must find the remainder after dividing by \(10^1\) (or \(10\)). You can accomplish this as follows:
cardNumber = 412831758;
accountType = cardNumber % 10; // Extract right-most 1 digit
To extract the issuing bank number you must extract the left-most three digits of a nine digit number. This means that you must divide by \(10^{9-3}\), or \(10^6\), or \(1000000\). This can be accomplished as follows:
cardNumber = 412831758;
issuer = cardNumber / 1000000; // Extract left-most 3 (of 9) digits
The part of the account number that identifies the account holder consists of the remaining digits. To get this part of the account number you must first drop the left-most three digits (i.e., you must find the remainder after dividing by \(10^{9-3}\)). Then, you must drop the right-most digit of the result (i.e., you must divide the result by \(10^1\)). This can be accomplished as follows:
cardNumber = 412831758;
holder = (cardNumber % 1000000) / 10;
A Warning
You need to be especially careful about the order in which you perform operations when using this pattern in a repeated fashion because they change the number of digits, \(N\). For example, when finding the account holder in the example above you had to first take the remainder after dividing by \(1000000\) and then divide by \(10\). Had you divided by \(10\) first, the intermediate value would have been \(41283175\) and the remainder after dividing by \(1000000\) would then have been \(283175\) instead of \(83175\).
Reversing the order of operations results in an incorrect solution because the intermediate value \(41283175\) only has \(8\) digits, not \(9\). So, to extract the right-most \(3\) digits you would have to take the remainder after dividing by \(10^{8-3}\) or (\(100000\)).
Looking Ahead
If you take a course on systems programming, you will probably encounter the following topics related to digit manipulation: working in other bases and bit shifting. Both are discussed briefly below.
Generalizing the Pattern
For reasons that may not be apparent now, hexadecimal (i.e., base 16) frequently arises in computing. Fortunately, this same pattern can be used with other bases. All that is needed is to replace \(10\) with the desired base, \(b\).
Bit Shifting
For reasons that hopefully are already apparent to you, binary (i.e.,
base 2) is also very important in computing. Many programming languages
(including Java) include the >> and << operators to shift the binary
representation of an integer value to the right or left a given number
of places. These lower-level operators are more relevant in a systems
programming course than an applications programming course, but will be
touched upon briefly at the end of Chapter
21
on segmented/packed arrays.



