Books / Introduction to Recursion and Backtracking / Chapter 4
Recursive Algorithms - Fibonacci Numbers
Recursion is not usually the most efficient solution, although it is usually the easiest to understand. One example of this is the Fibonacci sequence. The Fibonacci numbers are named after Leonardo de Pisa, who was known as Fibonacci. He did a population study of rabbits in which he simplified how they mated and how their population grew. In short, the idea is that rabbits never die, and they can mate starting at two months old, and that at the start of each month every rabbit pair gives birth to a male and a female (with very short gestation period!)
From these premises, it is not hard to show that the number of rabbit pairs in month 1 is 1, in month 2 is also 1 (since they are too young to mate), and in month 2, 2, since the pair mated and gave birth to a new pair. Let f(n) be the number of rabbits alive in month n. Then, in month n, where n > 2, the number of pairs must be the number of pairs alive in month n − 1, plus the number of new offspring born at the start of month n. All pairs alive in month n − 2 contribute their pair in month n, so there are f(n − 1) + f(n − 2) rabbit pairs alive in month n. The recursive definition of this sequence is thus:
\[f(n)= \begin{cases}1 & \text { if } n \leq 2 \\ f(n-1)+f(n-2) & \text { if } n>2\end{cases}\]This will generate the sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, and so on. A recursive algorithm to compute the nth Fibonacci number, for n > 0, is given below, written as a C/C++ function.
int fibonacci(int n) {
if (n <= 2)
return 1;
else
return fibonacci(n - 1) + fibonacci(n - 2);
}
Although this looks simple, it is very inefficient. If you write out a box trace of this function you will see that it leads to roughly \(2^{n}\) function calls to find the \(n^{t h}\) Fibonacci number. This is because it computes many values needlessly. There are far better ways to compute these numbers.
Fibonacci in Java and Recursion Tree
Let’s look at an example in Java and what the recursion tree looks like for it:
public int fib(int n) {
if(n <= 1) {
return n;
} else {
return fib(n - 1) + fib(n - 2);
}
}
The recursion tree for fib(5) is shown below.
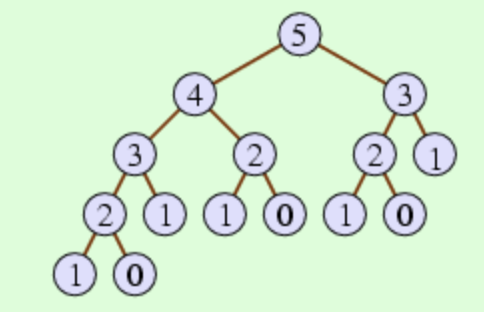
Recursion tree for computing fib(5).
The recursion tree has the original parameter (5 in this case) at the top, representing the original method invocation. In the case of fib(5), there would be two recursive calls, to fib(4) and fib(3), so we include 4 and 3 in our diagram below 5 and draw a line connecting them. Of course, fib(4) has two recursive calls itself, diagrammed in the recursion tree, as does fib(3). The complete diagram above depicts all the recursive invocation of fib made in the course of computing fib(5). The bottom of the recursion tree depicts those cases when there are no recursive calls — in this case, when n <= 1.



