Books / Introduction to Recursion and Backtracking / Chapter 12
Memoization
In general, recursion requires lots of function calls which requires creating and removing
lots of stack frames. This usually results in a lot of overhead and resources being used
to perform the computation. As depicted in the figure, several function calls are repeated: Fibonacci(3) is called
twice, Fibonacci(2) is called 3 times, etc. 15 total function calls are made to compute Fibonacci(5). In general, the computation of Fibonacci(n) will result in an exponential number of function calls.
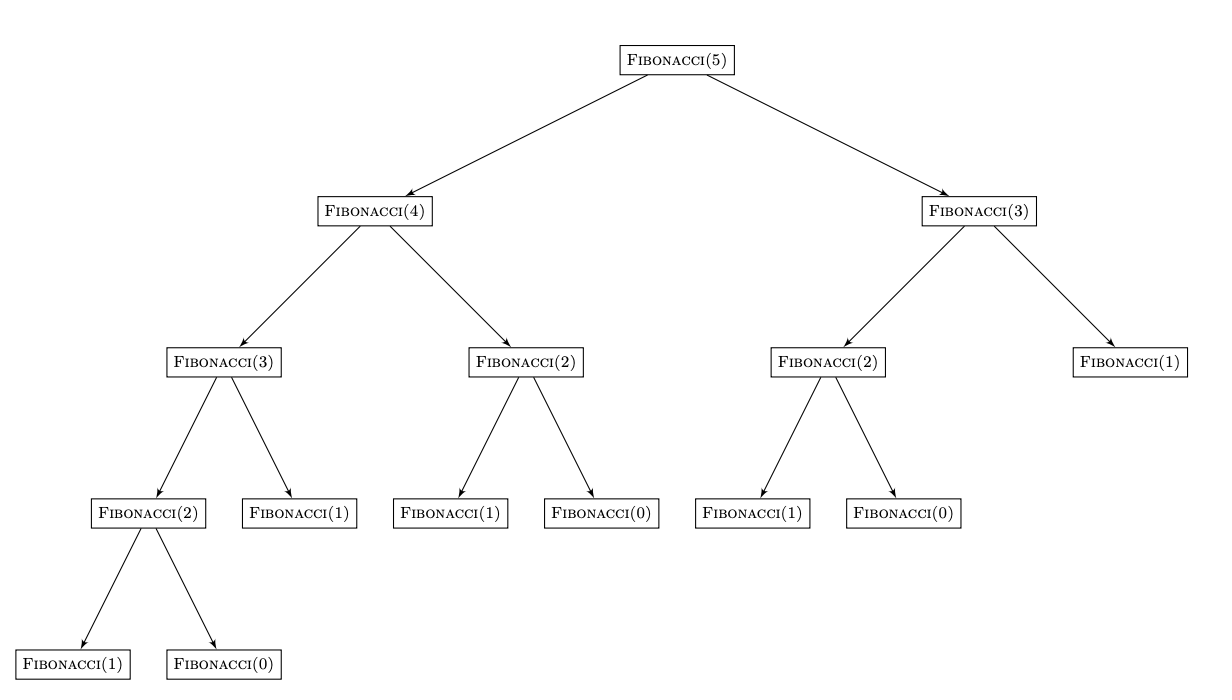
Figure 1 - Recursive Fibonacci Computation Tree
What if we wanted to compute F(100) = 573, 147, 844, 013, 817, 084, 101 (573 quintillion) it would result in 1,146,295,688,027,634,168,201 (1.146 sextillion) function calls. Using the same hardware, at 4.59 × 10^8 (459 million) function calls per second, it would take 2.497 × 1012 seconds to compute. That would be more than* 79,191 years! Even if we performed these (useless) calculations on hardware that was 1 million times faster than my laptop, it would still take over *4 weeks!
Memoization
The inefficiency in the example above comes from the fact that we make the same function calls on the same values over and over. One way to avoid recomputing the same values is to store them into a table. Then, when you need to compute a value, you look at the table to see if it has already been computed. If it has, we reuse the value stored in the table, otherwise we compute it by making the appropriate recursive calls. Once computed, we place the value into the table so that it can be looked up on subsequent function calls. This approach is usually referred to as memoization.
The “table” in this scenario is very general: it can be achieved using a number of different data structures including simple arrays, or even maps (mapping input value(s) to output values). The table is essentially serving as a cache for the previously computed values.
function fibonacci(n int) int {
// check if result already calculated
r = cache.get(n)
if r is not null {
return r
}
// If not already calculated, calculate and store
r = fibonacci(n-1) + fibonacci(n-2)
cache.store(n, r)
return r
}
// initialize cache with seed values
// cache.store(0, 0)
// cache.store(1, 1)
Summary
In this chapter, we looked an a optimization technique called memoization and how to use it to improve the performance of our recursive fibonacci calculating function in which a lot of calculations are repeated. Memoization simply remembers the result of a specific input. Subsequent calls with remembered inputs return the remembered results rather than recalculating it, which improves the performance.
Read our Memoization Guide for more information and examples.



