Books / Introduction to Recursion and Backtracking / Chapter 8
Tracing Recursion Using The Box Method
It is hard to trace how a recursive function works. You have to be systematic about it. There are a few established systems for doing this. One is called the box method. It is a visual way to trace a recursive function call.
The box trace helps us understand and visualize how a recursive call works.
The box method is a way to organize a trace of a recursive function. Each call is represented by a box containing the value parameters of the function, the local variables of the function, a place to store the return value of the function if it has a return value, placeholders for the return values of the recursive calls (if any), and a place for the return address. The steps are as follows.
Steps
- Label each recursive call in the function (e.g., with labels like 1,2,3,… or A,B,C,…). When a recursive call terminates, control returns to the instruction immediately following one of the labeled points. If it returns a value, that value is used in place of the function call.
- Create a box template, containing
- a placeholder for the value parameters of the parameter list,
- a placeholder for the local variables,
- a placeholder for each value returned by the recursive calls from the current call,
- a placeholder for the value returned by the function call.
- Now you start simulating the function’s execution. Write the instruction that calls the recursive function with the given arguments. For example, it might be:
System.out.println(factorial(3)); - Using your box template, create a box for the first call to the function. Draw an arrow from the instruction you wrote in step 3 to this first box.
- Execute the function by hand, updating values of local variables and reference parameters as needed. For each recursive call that the function makes, create a new box for that call, with an arrow from the old box to the box for the called function. Label the arrow with the label of the function being called.
- Repeat step 5 for each new box.
- Each time a function exits, if it has a return value, update the value in the box that called it, i.e., the one on the source side of the arrow, and then cross off the exiting box. Resume execution of the box that called the function at the instruction immediately following the label of the arrow.
We can trace the factorial function with this method to demonstrate the method. The factorial function has a single value parameter, n, and no local variables. It has a return value and a single recursive call. Its box should be:
n = ____
A: fact(n-1) = __
return = _______
Figure 1: Factorial Box Template
There are three placeholders, one for n, one for the return value of the recursive call, which is labeled A, and one for the return value of the function. The name of the function is abbreviated.
We trace the function for the call when the argument is 3 . The figure below illustrates the sequence of boxes. Each row represents a new step in the trace. The first row shows the initial box. The value of n is 3 . The other values are unknown. The function is called recursively so the next line shows two boxes. The box in bold is the one being traced. In that box, \(\mathrm{n}=2\), since it was called with \(\mathrm{n}-1\). That function calls factorial again, so in the next line there are three boxes. Eventually n becomes 0 in the fourth line. It does not make a recursive call. Instead it returns 1 and the box is deleted in the next line and the 1 sent to the fact(n-1) placeholder of the box that called it. This continues until the return values make their way back to the first box, which returns it to the calling program.
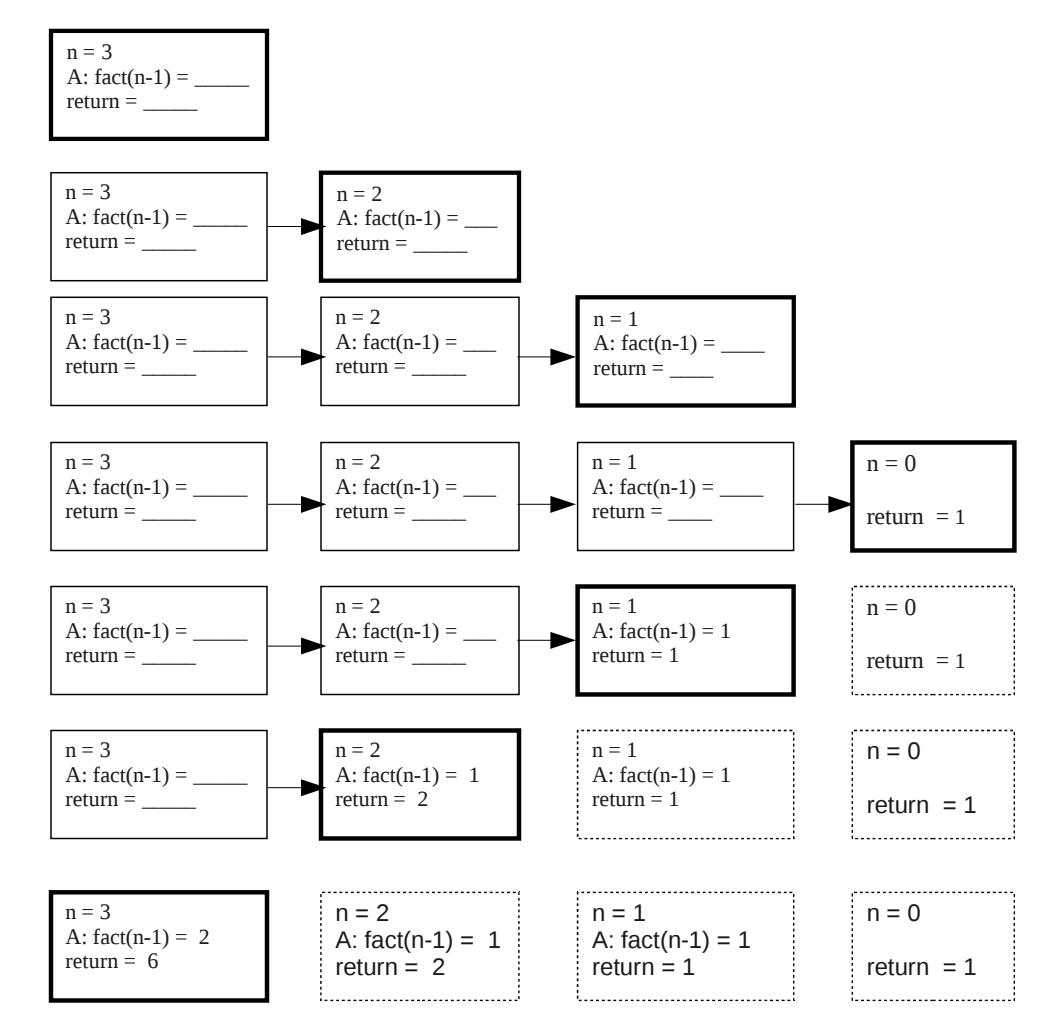
Figure 2. Box Trace of Factorial Function



