Books / Sorting Algorithms in Computer Science / Insertion Sort
Insertion Sort
Overview of Insertion Sort
Insertion sort is a sorting algorithm that builds the final sorted array (or list) one item at a time. It splits an array into a sorted and an unsorted regions. Elements are repeatedly picked from the unsorted region (starting with the lowest available index) and inserted into the proper position in the sorted region.
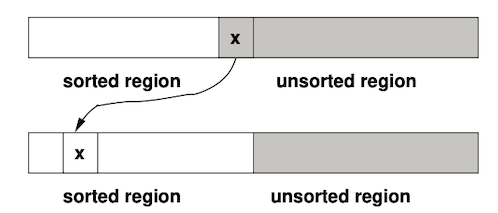
Insertion sort modeled as an array with a sorted and unsorted region. Each iteration moves the lowest-index value in the unsorted region into its position in the sorted region, which is initially of size 1
The process starts at the second position and stops when the rightmost element has been inserted, thereby forcing the size of the unsorted region to zero. It is like sorting a deck of cards to arrange them in the correct sequence, from smallest to largest. You take one card from the unsorted stack and put it in the right location in the sorted deck, moving other cards around it.
Characteristics of Insertion Sort
- Insertion sort is one of the simplest sorting algorithms.
- Insertion sort belongs to a class of sorting algorithms that sort by comparing keys to adjacent keys and swapping the items until they end up in the correct position. These sorts move items very slowly through the array, forcing them to move one position at a time until they reach their final destination.
- For the above reason, insertion sort will be inefficient for bigger arrays.
Insertion sort algorithm
Insertion sort splits an array into a sorted and an unsorted region, but unlike selection sort, it repeatedly picks the lowest index element of the unsorted region and inserts it into the proper position in the sorted region. Hence its name.
The insertion sort algorithm is below. It sorts the array from minimum to maximum.
int[] a = new int[]{3, 5, 7, 8, 1, 2, 2, 10};
for (int i = 1; i < a.length; i++) { // iterate through the entire array
int tmp = a[i]; // pick the current element to be sorted
int j;
for (j= i; j >= 1 && tmp < a[j - 1]; j = j - 1) { // look back and sort
a[j] = a[j - 1];
}
a[j] = tmp;
}
Output
[1, 2, 2, 3, 5, 7, 8, 10]
The step of assigning to tmp and then copying the value into its final position is a form of efficient swap. An ordinary swap takes three data moves; this reduces the swap to just one per item compared, plus the moves at the beginning and end of the loop. Let’s walk through this algorithm:
Pass number 1. Sorting a[1]=5
No swap occurred for this pass
Final array configuration for pass number 1:
[ 3 , 5 , 7 , 8 , 1 , 2 , 2 , 10 ]
Pass number 2. Sorting a[2]=7
No swap occurred for this pass
Final array configuration for pass number 2:
[ 3 , 5 , 7 , 8 , 1 , 2 , 2 , 10 ]
Pass number 3. Sorting a[3]=8
No swap occurred for this pass
Final array configuration for pass number 3:
[ 3 , 5 , 7 , 8 , 1 , 2 , 2 , 10 ]
Pass number 4. Sorting a[4]=1
[ 3 , 5 , 7 , 8 , 1 , 2 , 2 , 10 ] ==> [ 3 , 5 , 7 , 8 , 8 , 2 , 2 , 10 ]
[ 3 , 5 , 7 , 8 , 8 , 2 , 2 , 10 ] ==> [ 3 , 5 , 7 , 7 , 8 , 2 , 2 , 10 ]
[ 3 , 5 , 7 , 7 , 8 , 2 , 2 , 10 ] ==> [ 3 , 5 , 5 , 7 , 8 , 2 , 2 , 10 ]
[ 3 , 5 , 5 , 7 , 8 , 2 , 2 , 10 ] ==> [ 3 , 3 , 5 , 7 , 8 , 2 , 2 , 10 ]
Final array configuration for pass number 4:
[ 1 , 3 , 5 , 7 , 8 , 2 , 2 , 10 ]
Pass number 5. Sorting a[5]=2
[ 1 , 3 , 5 , 7 , 8 , 2 , 2 , 10 ] ==> [ 1 , 3 , 5 , 7 , 8 , 8 , 2 , 10 ]
[ 1 , 3 , 5 , 7 , 8 , 8 , 2 , 10 ] ==> [ 1 , 3 , 5 , 7 , 7 , 8 , 2 , 10 ]
[ 1 , 3 , 5 , 7 , 7 , 8 , 2 , 10 ] ==> [ 1 , 3 , 5 , 5 , 7 , 8 , 2 , 10 ]
[ 1 , 3 , 5 , 5 , 7 , 8 , 2 , 10 ] ==> [ 1 , 3 , 3 , 5 , 7 , 8 , 2 , 10 ]
Final array configuration for pass number 5:
[ 1 , 2 , 3 , 5 , 7 , 8 , 2 , 10 ]
Pass number 6. Sorting a[6]=2
[ 1 , 2 , 3 , 5 , 7 , 8 , 2 , 10 ] ==> [ 1 , 2 , 3 , 5 , 7 , 8 , 8 , 10 ]
[ 1 , 2 , 3 , 5 , 7 , 8 , 8 , 10 ] ==> [ 1 , 2 , 3 , 5 , 7 , 7 , 8 , 10 ]
[ 1 , 2 , 3 , 5 , 7 , 7 , 8 , 10 ] ==> [ 1 , 2 , 3 , 5 , 5 , 7 , 8 , 10 ]
[ 1 , 2 , 3 , 5 , 5 , 7 , 8 , 10 ] ==> [ 1 , 2 , 3 , 3 , 5 , 7 , 8 , 10 ]
Final array configuration for pass number 6:
[ 1 , 2 , 2 , 3 , 5 , 7 , 8 , 10 ]
Pass number 7. Sorting a[7]=10
No swap occurred for this pass
Final array configuration for pass number 7:
[ 1 , 2 , 2 , 3 , 5 , 7 , 8 , 10 ]
Time Complexity of Insertion Sort
The worst case number of comparisons and data moves is \(O\left(N^{2}\right)\) for an array of N elements. The best case is \(\Omega(N)\) data moves and \(\Omega(N)\) comparisons. We can prove that the average number of comparisons and data moves is \(\Omega\left(N^{2}\right)\).
Note: Big \(O\) is used to describe the worst case running time of an algorithm. \(\Omega\) is used for describing the best case running time of an algorithm.
Time Complexity of Insertion Sort vs Selection Sort
The worst case behavior of insertion sort is \(O\left(N^{2}\right)\). It moves much more data than selection sort, since selection sort moves O(N) data items as compared to insertion sort’s \(O\left(N^{2}\right)\) data exchanges. But insertion sort is natural; if the array is sorted initially, it will only perform 2(n − 1) data exchanges, and it is stable as implemented above, since elements with equal keys are never swapped with each other.
Common Insertion Sort Questions
1. Is insertion sort in place sorting algorithm?
Yes. Insertion sort belongs to a class of sorting algorithms that sort by comparing keys to adjacent keys and swapping the items until they end up in the correct position, that is, sort in place in the array. It sorts by moving items very slowly through the array, forcing them to move one position at a time until they reach their final destination. It stands to reason that the number of data moves would be excessive for the work accomplished. After all, there must be smarter ways to put elements into the correct position.
2. Is insertion sort adaptive?
Yes. In adaptive algorithms, the complexity (running time, performance) changes based on whether or not the input array is sorted. They perform better when the input is sorted. Insertion sort is adaptive because the initial order of the array has an impact on the number of operations. Partially sorted arrays would require fewer steps to sort.
3. Is insertion sort an efficient sorting algorithm?
No. Insertion sort moves element very slowly through an array and is not an efficient sorting algorithm for larger arrays.
4. What other sorting algorithms are like insertion sort?
Another sort that’s similar to insertion sort is the bubble sort.
Code Examples
Insertion sort in Java
public static void insertionSortInPlaceSwap(int[] a) {
for (int i = 1; i < a.length; i++) {
int j = i;
while (j > 0 && a[j - 1] > a[j]) {
swap(a, j, j - 1);
j--;
}
}
}
private static void swap(int[] a, int i, int j) {
int tmp = a[i];
a[i] = a[j];
a[i] = tmp;
}
Insertion sort in Python
def insertion_sort(arr):
for i in range(1, len(arr)):
# Set key:
key = arr[i]
j = i - 1
while j >= 0 and arr[j] > key:
# Swap:
arr[j + 1] = arr[j]
arr[j] = key
# Decrement 'j':
j -= 1
return arr
array = [5, 2, 12, 12, 1]
print("Original array: %s" % array)
print("Sorted array: %s" % insertion_sort(array))
Insertion Sort in C++
void InsertionSort(T A[], int n) {
// Precondition: A[0..n-1] contains the data to be sorted
// Postcondition: A[0..n-1] is sorted in ascending order.
// for each array element A[i], insert it into the sorted region
for (int i = 1; i < n; i++) {
// A[0..i-1] is in sorted order
tmp = A[i]; // copy
j = i;
while (j > 0 && tmp < A[j - 1]) {
A[j] = A[j - 1];
j--;
}
A[j] = tmp;
// A[0..i] is now sorted
}
}




Comments (1)
Rock Magar
Thank you..genuinely appreciate your effort to put this together in clean presentation and help me build my concepts.