Books / Sorting Algorithms in Computer Science / Shell Sort
Shell Sort
Overview of Shell Sort
Shell sort was invented by Donald Shell in 1959. It is a generalized version or an optimization of insertion sort. In insertion sort, many movements may be required to move an element. Shell sort optimizes that by sorting elements that are farther apart. By starting with far apart elements, it can move some out-of-place elements into position faster than a simple nearest neighbor exchange
Shell Sort Algorithm
Shell sort is like a sequence of insertion sorts carried out over varying distances in the array and has the advantage that in the early passes, it moves data items close to where they belong by swapping distant elements with each other.
Consider the original insertion sort modified so that the gap between adjacent elements can be a number besides 1:
int gap = 1;
for (int i = gap; i < a.size(); i++) {
tmp = a[i];
for (j = i; j >= gap && tmp < a[j - gap]; j = j - gap)
a[j] = a[j - gap];
a[j] = tmp;
}
Now suppose we let the variable gap start with a large value and get smaller with successive passes. Each pass is a modified form of insertion sort on each of a set of interleaved sequences in the array. When the gap is h, it is h insertion sorts on each of the h sequences. The idea is to arrange the list of elements so that, starting anywhere, taking every hth element produces a sorted list. Such a list is said to be h-sorted.
\[\begin{aligned} &0, h, 2 h, 3 h, \ldots, k_{0} h \\ &1,1+h, 1+2 h, 1+3 h, \ldots, 1+k_{1} h \\ &2,2+h, 2+2 h, 2+3 h, \ldots, 2+k_{2} h \\ &\cdots \\ &h-1, h-1+h, h-1+2 h, \ldots, h-1+k_{h-1} h \end{aligned}\]where \(k_{i}\) is the largest number such that \(i+k_{i} h<n\). For example, if the array size is 15, and the gap is h=5, then each of the following subsequences of indices in the array, which we will call slices, will be insertion-sorted independently:
slice 0: 0 5 10
slice 1: 1 6 11
slice 2: 2 7 12
slice 3: 3 8 13
slice 4: 4 9 14
For each fixed value of the gap, h, the sort starts at array element a[h] and inserts it in the lower sorted region of the slice, then it picks a[h+1] and inserts it in the sorted region of its slice, and then a[h+2] is inserted, and so on, until a[n-1] is inserted into its slice’s sorted region. For each element a[i], the sorted region of the slice is the set of array elements at indices i, i-h, i-2 h, … and so on. When the gap is h, we say that the array has been h-sorted. It is obviously not sorted, because the different slices can have different values, but each slice is sorted. Of course when the gap h=1 the array is fully sorted. The following table shows an array of 15 elements before and after a 5 -sort of the array.

The intuition is that the large initial gap sorts move items much closer to where they have to be, and then the successively smaller gaps move them closer to their final positions.
In Shell’s original algorithm the sequence of gaps was \(n / 2, n / 4, n / 8, \ldots, 1\). This proved to be a poor choice of gaps because the worst case running time was no better than ordinary insertion sort, as is proved below. Shell’s original algorithm is shown below:
for (int gap = a.size() / 2; gap > 0; gap /= 2)
for (int i = gap; i < a.size(); i++) {
tmp = a[i];
for (j = i; j >= gap && tmp < a[j - gap]; j = j - gap)
a[j] = a[j - gap];
a[j] = tmp;
}
Here’s Shell Sort implementation in Java:
public static void shellSort( Comparable[] a ){
for( int gap = a.length/2; gap > 0; gap = gap == 2 ? 1 : (int) ( gap / 2.2 ) ) {
for( int i = gap; i<a.length; i++ ) {
Comparable tmp = a[i];
int j = i;
for( ; j >= gap && tmp.compareTo( a[j - gap] ) < 0; j -= gap ) {
a[j] = a[j - gap];
}
a[j] = tmp;
}
}
}
Time and Space Complexity of Shell Sort Algorithm
Before going into details, here is a summary of time complexity of the shell sort algorithm. Please note that the running time of Shellsort is heavily dependent on the gap sequence it uses
-
Worst-case performance: Generally, it is \(O\left(N^{2}\right)\). (For best gap sequence, it could become: \(O\left(N Log^{2} N\right)\))
-
Best-case performance \(O\left(N Log N\right)\) for most gap sequences.
-
Worst-case space complexity: O(1)
Below is an in-depth and academic analysis of the running time of shell sort, if you are interested.
Analysis of Shell Sort Using Shell’s Original Increments
The running time of Shell Sort when the increment is \(h_{k}\) is \(O\left(n^{2} / h_{k}\right)\).
Proof: When the increment is \(h_{k}\), there are \(h_{k}\) insertion sorts of \(n / h_{k}\) keys. An insertion sort of m elements requires in the worst case \(O\left(m^{2}\right)\) steps. Therefore, when the increment is \(h_{k}\) the total number of steps is
\[h_{k} \cdot O\left(\frac{n^{2}}{h_{k}^{2}}\right)=O\left(\frac{n^{2}}{h_{k}}\right)\]The worst case for Shell Sort, using Shell’s original increment sequence, is \(\Theta\left(n^{2}\right)\).
Proof: The proof has two parts, one that the running time has a lower bound that is asymptotic to \(n^{2}\), and one that it has an upper bound of \(n^{2} .\)
Proof of Lower Bound
Consider any array of size \(n=2^{m}\), where m may be any positive integer. There are infinitely many of these, so this will establish asymptotic behavior. Let the n / 2 largest numbers be in the odd-numbered positions of the array and let the n / 2 smallest numbers be in the even numbered positions. When \(n\) is a power of 2 , halving the gap, which is initially \(n\), in each pass except the last, results in an even number. Therefore, in all passes of the algorithm until the very last pass, the gaps are even numbers, which implies that all of the smallest numbers must remain in even-numbered positions and all of the largest numbers will remain in the odd-numbered positions. When it is time to do the last pass, all of the n / 2 smallest numbers are sorted in the indices \(0,2,4,6,8, \ldots\), and the n / 2 largest numbers are sorted and in indices \(1,3,5,7\), and so on. This implies that the \(j^{t h}\) smallest number is in position \(2(j-1)\) (e.g., the second is in \(2 \cdot 2-2=2\) and the third is in \(2 \cdot 3-2=4\) ) and must be moved to position \(j-1\) when h=1. Therefore, this number must be moved \((2 j-2)-(j-1)=j-1\) positions. Moving all n / 2 smallest numbers to their correct positions when h=1 requires
\[\sum_{j=1}^{n / 2}(j-1)=\sum_{j=0}^{(n / 2)-1} j=\frac{(n / 2-1)(n / 2)}{2}=\Theta\left(n^{2}\right)\]steps. This proves that the running time is at least \(\Theta\left(n^{2}\right)\).
Proof of Upper Bound
As we’ve already seen, the running time of the pass when the increment is \(h_{k}\) is \(O\left(n^{2} / h_{k}\right)\). Suppose there are \(t\) passes of the sort. If we sum over all passes, we have for the total running time,
\[O\left(\sum_{k=1}^{t} \frac{n^{2}}{h_{k}}\right)=O\left(n^{2} \sum_{k=1}^{t} \frac{1}{h_{k}}\right)=O\left(n^{2} \sum_{k=1}^{t} \frac{1}{2^{k}}\right)=O\left(n^{2}\right)\]This shows that \(n^{2}\) is an asymptotic upper bound as well. It follows that the worst case is \(\Theta\left(n^{2}\right)\)
Other Increment Schemes
Better choices of gap sequences were found after Shell’s initial publication of the algorithm. Before looking at some of the good ones, consider an example using a simple sequence such as 5,3,1.
Example
This uses the three gaps, 5,3,1 on an arbitrary array whose initial state is on the first row in the table below.

Hibbard proposed using the sequence:
\[h_{1}=1, h_{2}=3, h_{3}=7, h_{4}=15, \ldots, h_{t}=2^{t}-1\]which is simply the numbers one less than powers of 2 . Such a sequence, 1,3,7,15,31,63,127, ..., has the property that no two adjacent terms have a common factor: if they had a common factor p, then their difference would also be divisible by \(x^{1}\) But the difference between successive terms is \(\left(2^{k+1}-1\right)-\left(2^{k}-1\right)=\left(2^{k+1}-2^{k}\right)=2^{k}\) which is divisible by powers of 2 alone. Hence the only number that can divide successive terms is a power of 2 . Since all of the terms are odd numbers, none are divisible by 2 , so they have no common factor.
Successive terms are related by the recurrence
\[h_{k+1}=2 h_{k}+1\]Sedgewick proposed a few different sequences, such as this one, defined recursively:
\[h_{1}=1, h_{k+1}=3 h_{k}+1\]which generates the sequence
1,4,13,40,121,364, ...
This sequence has a worst case running time of \(\Theta\left(n^{4 / 3}\right)\). Hibbard’s increment sequence turns out to be an improvement over Shell’s original increment sequence.
The worst case running time of Shell Sort using Hibbard’s sequence, \(h_{1}=1, h_{2}=\) \(3, h_{3}=7, h_{4}=15, \ldots, h_{t}=2^{t}-1\), is \(\Theta\left(n^{3 / 2}\right)\)
Proof: Because this states the bound using \(\Theta()\) notation, we need to show that the running time grows no faster than \(n^{3 / 2}\) and also that it grows no slower than it. The first part requires showing that \(n^{3 / 2}\) is an asymptotic upper bound on the worst case running time. The second part requires showing that it is an asymptotic lower bound on the worst case running time.
\({ }^{1}\) If \(a\) and \(b\) are two integers with a common factor p, then there are two integers \(r\) and \(q\) such that \(a=q p\) and \(b=r p\). Then \(a-b=q p-r p=(q-r) p\), showing that the difference has this same common factor. The asymptotic upper bound alone is proved here. Proving the lower bound requires showing that there is some input array such that the algorithm’s running time will be proportional to \(n^{3 / 2}\). As the upper bound shows it is at most \(n^{3 / 2}\) and the lower bound shows at least one array requires \(n^{3 / 2}\) time, this establishes that it is \(\Theta\left(n^{3 / 2}\right)\).
As we have already established that the running time of a pass when the increment is \(h_{k}\) is \(O\left(n^{2} / h_{k}\right)\). We will use this fact for all increments \(h_{k}\) such that \(h_{k}>n^{1 / 2}\). This is not a tight enough upper bound for the smaller increments, and we need to work harder to get a tighter bound for them. The general idea will be to show that by the time the increments are that small, most elements do not need to be moved very far.
So we turn to the case when \(h_{k} \leq n^{1 / 2}\). By the time that the array is \(h_{k}\)-sorted, it has already been \(h_{k+1}\)-sorted and \(h_{k+2}\)-sorted. Now consider the array elements at positions p and \(p-i\) for all \(i \leq p\). If \(i\) is a multiple of \(h_{k+1}\) or \(h_{k+2}\), then \(a[p-i]<a[p]\) because these two elements were part of the same slice, either for increment \(h_{k+1}\) or increment \(h_{k+2}\), and so they were sorted with respect to each other. More generally, suppose that \(i\) is a non-negative linear combination of \(h_{k+1}\) and \(h_{k+2}\), i.e., \(i=c_{1} h_{k+1}+c_{2} h_{k+2}\), for some non-negative integers \(c_{1}\) and \(c_{2}\). Then
\[p-i=p-\left(c_{1} h_{k+1}+c_{2} h_{k+2}\right)=p-c_{1} h_{k+1}-c_{2} h_{k+2}\]and
\[(p-i)+c_{2} h_{k+2}=p-c_{1} h_{k+1}\]which implies that after the \(h_{k+2}\)-sort, \(a[p-i]<a\left[p-c_{1} h_{k+1}\right]\) because they are part of the same \(h_{k+2}\)-slice. Similarly, after the \(h_{k+1}\)-sort, \(a\left[p-c_{1} h_{k+1}\right]<a[p]\) because they are part of the same \(h_{k+1}\)-slice and \(p-c_{1} h_{k+1}<p\). Thus, \(a[p-i]<a\left[p-c_{1} h_{k+1}\right]<a[p]\).
Since \(h_{k+2}=2 h_{k+1}\) by the definition of Shell’s increment scheme, \(h_{k+2}\) and \(h_{k+1}\) are relatively prime. (If not, they have a common factor \(>1\) and so their difference \(h_{k+2}-h_{k+1}=2 h_{k+1}+1-h_{k+1}=\) \(h_{k+1}+1\) would have a common factor with each of them, and in particular \(h_{k+1}\) and \(h_{k+1}+1\) would have a common factor, which is impossible.) Because \(h_{k+2}\) and \(h_{k+1}\) are relatively prime, their greatest common divisor (gcd) is 1. An established theorem of number theory is that if \(c=\operatorname{gcd}(x, y)\) then there are integers \(a\) and \(b\) such that \(c=a x+b y\). When \(x\) and \(y\) are relatively prime, this implies that there exist \(a, b\) such that \(1=a x+b y\), which further implies that every integer can be expressed as a linear combination of \(x\) and \(y\). A stronger result is that all integers at least as large as \((x-1)(y-1)\) can be expressed as non-negative linear combinations of \(x\) and \(y\). Let
\[\begin{aligned} m & \geq\left(h_{k+2}-1\right)\left(h_{k+1}-1\right) \\ &=\left(2 h_{k+1}+1-1\right)\left(2 h_{k}+1-1\right) \\ &=2\left(h_{k+1}\right)\left(2 h_{k}\right) \\ &=4 h_{k}\left(2 h_{k}+1\right)=8 h_{k}^{2}+4 h_{k} \end{aligned}\]By the preceding statement, m can be expressed in the form \(c_{1} h_{k+1}+c_{2} h_{k+2}\) for non-negative integers \(c_{1}\) and \(c_{2}\). From the preceding discussion, we can also conclude that \(a[p-m]<a[p]\). What does this mean? For any number \(i \geq 8 h_{k}^{2}+4 h_{k}, a[p-i]<a[p]\). Or stated the other way, \(a[p]\) is definitely larger than all elements in its \(h_{k}\)-slice below \(a\left[p-\left(8 h_{k}^{2}+4 h_{k}\right)\right]\), so the furthest it would have to be moved is \(8 h_{k}^{2}+4 h_{k}\) cells down. Therefore, during the \(h_{k}\)-sort, no element has to be moved more than \(8 h_{k}-4\) times (since each moves in \(h_{k}\) increments each time.) There are at most \(n-h_{k}\) such positions, and so the total number of comparisons in this pass is \(O\left(n h_{k}\right) .\)
How many increments \(h_{k}\) are smaller than \(n^{1 / 2} ?\) Roughly half of them, because if we approximate \(n\) as a power of 2 , say \(2^{t}\), then \(\sqrt{n}=2^{t / 2}\) and the increments \(1,3,7, \ldots, 2^{t / 2}-1\) are half of the total number of increments. For simplicity, assume \(t\) is an even number. Then the total running time of Shell Sort is
\[\begin{aligned} & O\left(\sum_{k=1}^{t / 2} n h_{k}+\sum_{k=t / 2+1}^{t} \frac{n^{2}}{h_{k}}\right) \\ =& O\left(n \sum_{k=1}^{t / 2} h_{k}+n^{2} \sum_{k=t / 2+1}^{t} \frac{1}{h_{k}}\right) \end{aligned}\]Now we have
\[\begin{aligned} n \sum_{k=1}^{t / 2} h_{k} &=n\left(1+3+7+\cdots+2^{t / 2}-\right.\\ &<n\left(1+4+8+\cdots+2^{t / 2}\right) \\ &=n \sum_{k=1}^{t / 2} 2^{k} \\ &=n \cdot\left(2^{t / 2+1}-1\right) \\ &<n \cdot 2 \sqrt{n} \\ &=2 n^{3 / 2} \end{aligned}\]which shows that the first sum is \(O\left(n \cdot n^{1 / 2}\right)=O\left(n^{3 / 2}\right)\). Since \(h_{t / 2+1}=\Theta\left(n^{1 / 2}\right)\), the second sum can be written as
\[\begin{aligned} n^{2} \sum_{k=t / 2+1}^{t} \frac{1}{h_{k}} &=n^{2}\left(\frac{1}{2^{t / 2+1}-1}+\frac{1}{2^{t / 2+2}-1}+\cdots+\frac{1}{2^{t}-1}\right) \\ &=n^{2}\left(\frac{1}{2 \sqrt{n}-1}+\frac{1}{4 \sqrt{n}-1}+\cdots+\frac{1}{2^{t / 2} \sqrt{n}-1}\right) \\ & \approx n^{2} \cdot \frac{1}{\sqrt{n}}\left(\frac{1}{2}+\frac{1}{4}+\cdots+\frac{1}{2^{t / 2}}\right) \\ &<2 n^{3 / 2} \end{aligned}\]which shows that the second sum is also \(O\left(n^{3 / 2}\right)\). This shows that the upper bound in the worst case running time using Hibbard’s sequence is \(O\left(n^{3 / 2}\right)\). The lower bound proof, i.e., that there is a sequence that achieves it is an exercise.
Many other sequences have been studied. Studies have shown that the sequence defined by
\[\left(h_{i}, h_{i+1}\right)=\left(9 \cdot\left(4^{i-1}-2^{i-1}\right)+1,4^{i+1}-6 \cdot 2^{i}+1\right) i=1,2, \ldots\]which generates 1,5,19,41,109, ... has \(O\left(n^{4 / 3}\right)\) worst case running time (Sedgewick, 1986). The notation above means that the formula generates pairs of gaps.
Example:
This shows how Shell sort works on an array using the gap sequence 13,4,1:
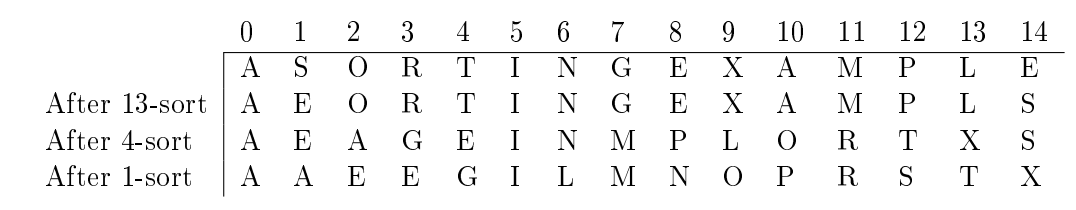
This shows how Shell sort works on an array using the gap sequence 13,4,1



