Example of Depth-First Search (DFS) algorithm in Java

Depth-first Search

A very common and natural way to traverse a graph, directed or undirected, is analogous to a pre-order traversal of a binary tree and it is called a depth-first search, or DFS for short. DFS is a backtrack-style traversal that visits a node and then recursively visits all nodes adjacent to it that have not yet been visited. To prevent the algorithm from going into an endless loop by revisiting nodes, when a node is visited for the first time it is marked.

Here’s an animation showing Depth-first search traversing through a tree.

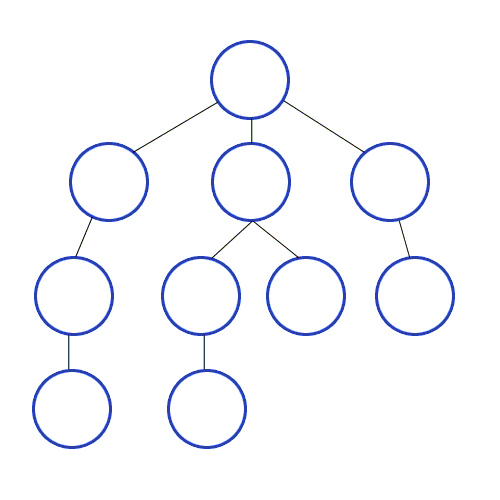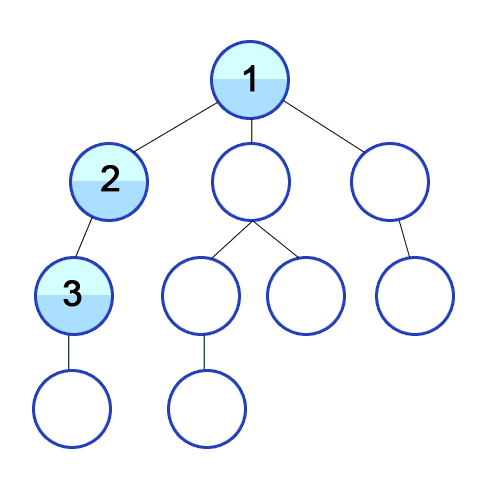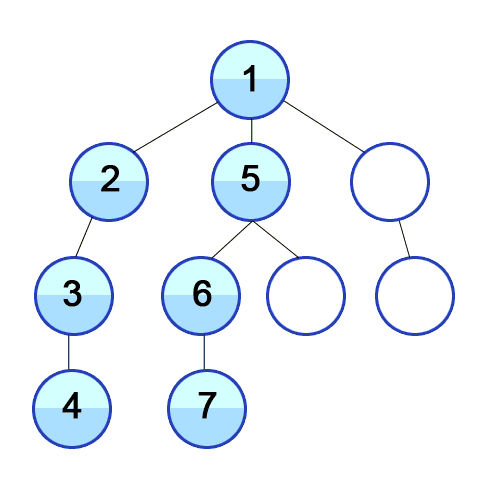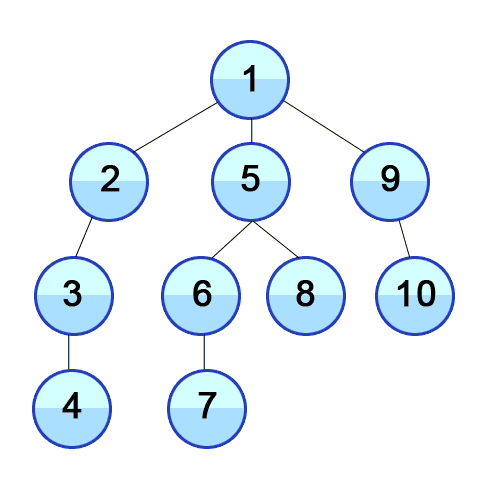
For this example, our graph has 8 nodes, A through H:

• A has an edge to node B.
• B has an edge to node G.
• B has edges to nodes C and D.
• C has an edge to node D.
• D has an edge to node E.
• E has edges to nodes F and G.
• G has an edge to node H.

DFS using Recursion

import java.util.LinkedList;

// Class to represent a node in the graph
class Node {
    String name;
    LinkedList<Node> neighbors;
    boolean visited;

    public Node(String name) {
        this.name = name;
        this.neighbors = new LinkedList<>();
        this.visited = false;
    }
}

public class DepthFirstSearch {
    public static void main(String[] args) {
        // Create eight nodes
        Node A = new Node("A");
        Node B = new Node("B");
        Node C = new Node("C");
        Node D = new Node("D");
        Node E = new Node("E");
        Node F = new Node("F");
        Node G = new Node("G");
        Node H = new Node("H");

        // Add edges: A -> B
        A.neighbors.add(B);
        // B -> G, B -> C, B -> D
        B.neighbors.add(G);
        B.neighbors.add(C);
        B.neighbors.add(D);
        // C -> D
        C.neighbors.add(D);
        // D -> E
        D.neighbors.add(E);
        // E -> F, E -> G
        E.neighbors.add(F);
        E.neighbors.add(G);
        // G -> H
        G.neighbors.add(H);

        // Put all nodes in a linked list
        Node[] nodes = {A, B, C, D, E, F, G, H};

        // Perform DFS starting from node A
        dfs(A);
    }

    public static void dfs(Node node) {
        // Mark the current node as visited
        node.visited = true;
        System.out.print(node.name + " ");

        // Recursively visit all unvisited neighbors
        for (Node neighbor : node.neighbors) {
            if (!neighbor.visited) {
                dfs(neighbor);
            }
        }
    }
}

This prints:

A B G H C D E F 

Here, the the DFS algorithm starts at node A and visits its neighbors B, G, H, C, D, E, F in that order

• Our DFS algorithm starts at node A and visits its only neighbor: node B.
• Then the algorithm visits node G, which is a neighbor of B, and then node H, which is a neighbor of G.
• After visiting all the nodes reachable from node A, the algorithm backtracks to node B and visits its other neighbor: node C.
• Node C has a neighbor, node D, which the algorithm then visits.
• Finally, the algorithm backtracks to node E and visits its neighbors, nodes F and G, in that order.

The isVisited variable is used to keep a track of which nodes have been visited by the DFS algorithm already. It is important to mark a node as visited when it is first encountered, as this helps the algorithm avoid visiting the same node multiple times and getting stuck in an infinite loop. For example if we have the following graph:

A -- B
|    |
C -- D

If we start the DFS algorithm at node A and do not mark nodes as visited, the algorithm will visit node B and then follow the the graph through nodes D and C back to A. It will then repeat indefinitely and will get stuck in an infinite loop. This is why we must mark nodes as visited.

Iterative DFS without using Recursion

Alternatively, we can implement DFS without recursion using a Stack. The dfsIterative() method below takes a starting node as its argument and then performs DFS on the graph starting from that node. It uses Stack data structure to store the nodes that need to be visited and marks each node as visited after visiting them. It uses Stack (as opposed to Queue) because DFS explores the depth of the graph first before exploring its breadth.

public static void dfsIterative(Node start) {
    Stack<Node> stack = new Stack<>();
    stack.push(start);
    start.visited = true;

    while (!stack.isEmpty()) {
        Node current = stack.pop();
        System.out.print(current.name + " ");

        for (Node neighbor : current.neighbors) {
            if (!neighbor.visited) {
                stack.push(neighbor);
                neighbor.visited = true;
            }
        }
    }
}

Related Questions