A red-black tree is a 2–3–4 tree (i.e. all nodes have 2, 3, or 4 children and 1, 2, or 3 internal keys) where each node is represented by a little binary tree with a black root and zero, one, or two red extender nodes as follows:

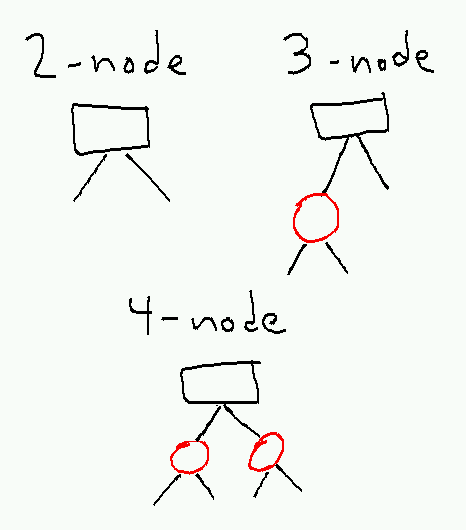
The invariant for a red-black tree is that

1. No two red nodes are adjacent.
2. Every path contains the same number of black nodes.

For technical reasons, we include the null pointers at the bottom of the tree as black nodes; this has no effect on the invariant, but simplifies the description of the rebalancing procedure.

From the invariant it follows that every path has between k and 2k nodes, where k is the black-height, the common number of black nodes on each path. From this we can prove that the height of the tree is O(log n).

Searching in a red-black tree is identical to searching in any other binary search tree; we simply ignore the color bit on each node. So search takes O(log n) time. For insertions, we use the standard binary search tree insertion algorithm, and insert the new node as a red node. This may violate the first part of the invariant (it doesn’t violate the second because it doesn’t change the number of black nodes on any path). In this case we need to fix up the constraint by recoloring nodes and possibly performing a single or double rotation.

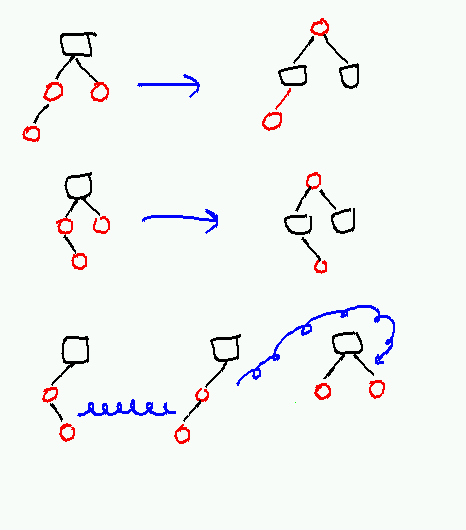
Which operations we need to do depend on the color of the new node’s uncle. If the uncle is red, we can recolor the node’s parent, uncle, and grandparent and get rid of the double-red edge between the new node and its parent without changing the number of black nodes on any path. In this case, the grandparent becomes red, which may create a new double-red edge which must be fixed recursively. Thus up to O(log n) such recolorings may occur at a total cost of O(log n).

If the uncle is black (which includes the case where the uncle is a null pointer), a rotation (possibly a double rotation) and recoloring is necessary. In this case (depicted at the bottom of the picture above), the new grandparent is always black, so there are no more double-red edges. So at most two rotations occur after any insertion.

Deletion is more complicated but can also be done in O(log n) recolorings and O(1) (in this case up to 3) rotations. Because deletion is simpler in red-black trees than in AVL trees, and because operations on red-black trees tend to have slightly smaller constants than corresponding operation on AVL trees, red-black trees are more often used that AVL trees in practice.

---

---