Books / Introduction to C Programming Language / Chapter 41
B trees
Neither is used as much as a B-tree, a specialized data structure optimized for storage systems where the cost of reading or writing a large block (of typically 4096 or 8192 bytes) is no greater than the cost of reading or writing a single bit. Such systems include typical disk drives, where the disk drive has to spend so long finding data on disk that it tries to amortize the huge (tens of millions of CPU clock cycles) seek cost over many returned bytes.
A B-tree is a generalization of a 2–3 tree where the root has at most M − 1 keys, and each node has between M/2 and M − 1 keys, where M is some large constant chosen so that a node (including up to M pointers and up to M − 1 keys) will just fit inside a single block. When a node would otherwise end up with M keys, it splits into two nodes with M/2 keys each, and moves its middle key up into its parent. As in 2–3 trees this may eventually require the root to split and a new root to be created; in practice, M is often large enough that a small fixed height is enough to span as much data as the storage system is capable of holding.
Searches in B-trees require looking through logM^n nodes, at a cost of O(M) time per node. If M is a constant the total time is asymptotically O(log n). But the reason for using B-trees is that the O(M) cost of reading a block is trivial compare to the much larger constant time to find the block on the disk; and so it is better to minimize the number of disk accesses (by making M large) than reduce the CPU time.
Deletions in B-trees are a nuisance. Deleting a key within a node that has only M/2 keys requires are rotation that steals a key from one of its siblings. If this would cause the sibling to drop below M/2 as well, the two nodes are merged. Merging two siblings steals a key from the parent, which may require further tinkering higher up in the tree. This means that deleting a key from a B-tree will require modifying O(log n) nodes in the worst case.
Below is a rudimentary B-tree implementation that provides only insert and search. For practical use you should probably for an existing B-tree library that has been tuned for whatever programming environment and system you are working on.
/* implementation of a B-tree */
typedef struct btNode *bTree;
/* create a new empty tree */
bTree btCreate(void);
/* free a tree */
void btDestroy(bTree t);
/* return nonzero if key is present in tree */
int btSearch(bTree t, int key);
/* insert a new element into a tree */
void btInsert(bTree t, int key);
/* print all keys of the tree in order */
void btPrintKeys(bTree t);
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <string.h>
#include "bTree.h"
#define MAX_KEYS (1024)
struct btNode {
int isLeaf; /* is this a leaf node? */
int numKeys; /* how many keys does this node contain? */
int keys[MAX_KEYS];
struct btNode *kids[MAX_KEYS+1]; /* kids[i] holds nodes < keys[i] */
};
bTree
btCreate(void)
{
bTree b;
b = malloc(sizeof(*b));
assert(b);
b->isLeaf = 1;
b->numKeys = 0;
return b;
}
void
btDestroy(bTree b)
{
int i;
if(!b->isLeaf) {
for(i = 0; i < b->numKeys + 1; i++) {
btDestroy(b->kids[i]);
}
}
free(b);
}
/* return smallest index i in sorted array such that key <= a[i] */
/* (or n if there is no such index) */
static int
searchKey(int n, const int *a, int key)
{
int lo;
int hi;
int mid;
/* invariant: a[lo] < key <= a[hi] */
lo = -1;
hi = n;
while(lo + 1 < hi) {
mid = (lo+hi)/2;
if(a[mid] == key) {
return mid;
} else if(a[mid] < key) {
lo = mid;
} else {
hi = mid;
}
}
return hi;
}
int
btSearch(bTree b, int key)
{
int pos;
/* have to check for empty tree */
if(b->numKeys == 0) {
return 0;
}
/* look for smallest position that key fits below */
pos = searchKey(b->numKeys, b->keys, key);
if(pos < b->numKeys && b->keys[pos] == key) {
return 1;
} else {
return(!b->isLeaf && btSearch(b->kids[pos], key));
}
}
/* insert a new key into a tree */
/* returns new right sibling if the node splits */
/* and puts the median in *median */
/* else returns 0 */
static bTree
btInsertInternal(bTree b, int key, int *median)
{
int pos;
int mid;
bTree b2;
pos = searchKey(b->numKeys, b->keys, key);
if(pos < b->numKeys && b->keys[pos] == key) {
/* nothing to do */
return 0;
}
if(b->isLeaf) {
/* everybody above pos moves up one space */
memmove(&b->keys[pos+1], &b->keys[pos], sizeof(*(b->keys)) * (b->numKeys - pos));
b->keys[pos] = key;
b->numKeys++;
} else {
/* insert in child */
b2 = btInsertInternal(b->kids[pos], key, &mid);
/* maybe insert a new key in b */
if(b2) {
/* every key above pos moves up one space */
memmove(&b->keys[pos+1], &b->keys[pos], sizeof(*(b->keys)) * (b->numKeys - pos));
/* new kid goes in pos + 1*/
memmove(&b->kids[pos+2], &b->kids[pos+1], sizeof(*(b->kids)) * (b->numKeys - pos));
b->keys[pos] = mid;
b->kids[pos+1] = b2;
b->numKeys++;
}
}
/* we waste a tiny bit of space by splitting now
* instead of on next insert */
if(b->numKeys >= MAX_KEYS) {
mid = b->numKeys/2;
*median = b->keys[mid];
/* make a new node for keys > median */
/* picture is:
*
* 3 5 7
* A B C D
*
* becomes
* (5)
* 3 7
* A B C D
*/
b2 = malloc(sizeof(*b2));
b2->numKeys = b->numKeys - mid - 1;
b2->isLeaf = b->isLeaf;
memmove(b2->keys, &b->keys[mid+1], sizeof(*(b->keys)) * b2->numKeys);
if(!b->isLeaf) {
memmove(b2->kids, &b->kids[mid+1], sizeof(*(b->kids)) * (b2->numKeys + 1));
}
b->numKeys = mid;
return b2;
} else {
return 0;
}
}
void
btInsert(bTree b, int key)
{
bTree b1; /* new left child */
bTree b2; /* new right child */
int median;
b2 = btInsertInternal(b, key, &median);
if(b2) {
/* basic issue here is that we are at the root */
/* so if we split, we have to make a new root */
b1 = malloc(sizeof(*b1));
assert(b1);
/* copy root to b1 */
memmove(b1, b, sizeof(*b));
/* make root point to b1 and b2 */
b->numKeys = 1;
b->isLeaf = 0;
b->keys[0] = median;
b->kids[0] = b1;
b->kids[1] = b2;
}
}
Splay trees
Yet another approach to balancing is to do it dynamically. Splay trees, described by Sleator and Tarjan in the paper “Self-adjusting binary search trees” (JACM 32(3):652–686, July 1985) are binary search trees in which every search operation rotates the target to the root. If this is done correctly, the amortized cost of each tree operation is O(log n), although particular rare operations might take as much as O(n) time. Splay trees require no extra space because they store no balancing information; however, the constant factors on searches can be larger because every search requires restructuring the tree. For some applications this additional cost is balanced by the splay tree’s ability to adapt to data access patterns; if some elements of the tree are hit more often than others, these elements will tend to migrate to the top, and the cost of a typical search will drop to O(log m), where m is the size of the “working set” of frequently-accessed elements.
How splaying works
The basic idea of a splay operation is that we move some particular node to the root of the tree, using a sequence of rotations that tends to fix the balance of the tree if the node starts out very deep. So while we might occasionally drive the tree into a state that is highly unbalanced, as soon as we try to exploit this by searching for a deep node, we’ll start balancing the tree so that we can’t collect too much additional cost. In fact, in order to set up the bad state in the first place we will have to do a lot of cheap splaying operations: the missing cost of these cheap splays ends up paying for the cost of the later expensive search.
Splaying a node to the root involves performing rotations two layers at a time. There are two main cases, depending on whether the node’s parent and grandparent are in the same direction (zig-zig) or in opposite directions (zig-zag), plus a third case when the node is only one step away from the root. At each step, we pick one of these cases and apply it, until the target node reaches the root of the tree.
This is probably best understood by looking at a figure from the original paper:
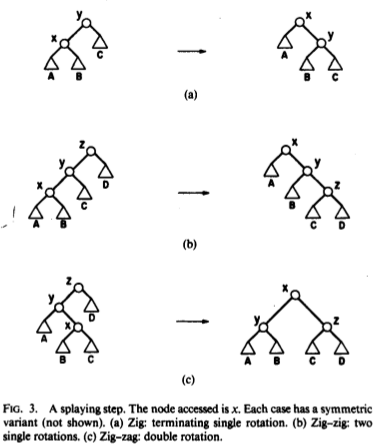
The bottom two cases are the ones we will do most of the time.
Just looking at the picture, it doesn’t seem like zig-zig will improve balance much. But if we have a long path made up of zig-zig cases, each operation will push at least one node off of this path, cutting the length of the path in half. So the rebalancing happens as much because we are pushing nodes off of the long path as because the specific rotation operations improve things locally.
Analysis
Sleator and Tarjan show that any sequence of m splay operations on an n-node splay tree has total cost at most O((m + n)log n + m). For large m (at least linear in n), the O(mlog n) term dominates, giving an amortized cost per operation of O(log n), the same as we get from any balanced binary tree. This immediately gives a bound on search costs, because the cost of plunging down the tree to find the node we are looking for is proportional to the cost of splaying it up to the root.
Splay trees have a useful “caching” property in that they pull frequently-accessed nodes to the to the top and push less-frequently-accessed nodes down. The authors show that if only k of the n nodes are accessed, the long-run amortized cost per search drops to O(log k). For more general access sequences, it is conjectured that the cost to perform a sufficiently long sequence of searches using a splay tree is in fact optimal up to a constant factor (the “dynamic optimality conjecture”), but no one has yet been able to prove this conjecture (or provide a counterexample).
Other operations
A search operation consists of a standard binary tree search followed by splaying the target node to the root (if present) or the last non-null node we reached to the root instead (if not).
Insertion and deletion are built on top of procedures to split and join trees.
A split divides a single splay tree into two splay trees, consisting of all elements less than or equal to some value x and all elements greater than x. This is done by searching for x, which brings either x or the first element less than or greater than x to the root, then breaking the link between the root and its left or right child depending on whether the root should go in the right or left tree.
A join merges two splay trees L and R, where every element in L is less than every element in R. This involves splaying the largest element in L to the root, and then making the root of R the right child of this element.
To do an insert of x, we do a split around x, then make the roots of the two trees the children of a new element holding x (unless x is already present in the tree, in which case we stop before breaking the trees apart).
To do a delete of an element x, we splay x to the root, remove it, then join the two orphaned subtrees.
For each operation, we are doing a constant number of splays (amortized cost O(log n) each), plus O(1) additional work. A bit of work is needed to ensure that the joins and splits don’t break the amortized cost analysis, but this is done in the paper, so we will sweep it under the carpet with the rest of the analysis.
Top-down splaying
There are a few remaining details that we need to deal with before trying to implement a splay trees. Because the splay tree could become very deep, we probably don’t want to implement a splay recursively in a language like C, because we’ll blow out our stack. We also have a problem if we are trying to rotate our target up from the bottom of figuring out what its ancestors are. We could solve both of these problems by including parent pointers in our tree, but this would add a lot of complexity and negate the space improvement over AVL trees of not having to store heights.
The solution given in the Sleator-Tarjan paper is to replace the bottom-up splay procedure with a top-down splay procedure that accomplishes the same task. The idea is that rotating a node up from the bottom effectively splits the tree above it into two new left and right subtrees by pushing ancestors sideways according to the zig-zig and zig-zag patters. But we can recognize these zig-zig and zig-zag patterns from the top as well, and so we can construct these same left and right subtrees from the top down instead of the bottom up. When we do this, instead of adding new nodes to the tops of the trees, we will be adding new nodes to the bottoms, as the right child of the rightmost node in the left tree or the left child of the rightmost node in the left tree.
Here’s the picture, from the original paper:
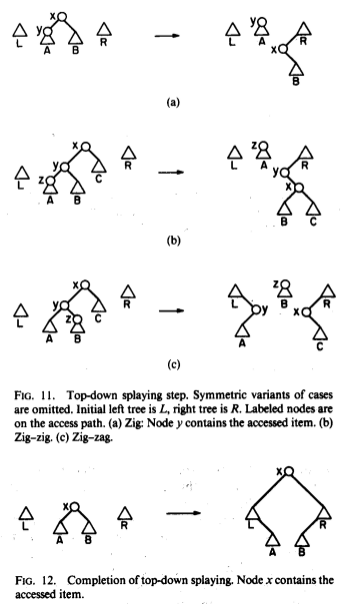
To implement this, we need to keep track of the roots of the three trees, as well as the locations in the left and right trees where we will be adding new vertices. The roots we can just keep pointers to. For the lower corners of the trees, it makes sense to store instead a pointer to the pointer location, so that we can modify the pointer in the tree (and then move the pointer to point to the pointer in the new corner). Initially, these corner pointers will just point to the left and right tree roots, which will start out empty.
The last step (shown as Figure 12 from the paper) pastes the tree back together by inserting the left and right trees between the new root and its children.
An implementation
Here is an implementation of a splay tree, with an interface similar to the previous AVL tree implementation.
/*
* Basic binary search tree data structure without balancing info.
*
* Convention:
*
* Operations that update a tree are passed a struct tree **,
* so they can replace the argument with the return value.
*
* Operations that do not update the tree get a const struct tree *.
*/
#define LEFT (0)
#define RIGHT (1)
#define TREE_NUM_CHILDREN (2)
struct tree {
/* we'll make this an array so that we can make some operations symmetric */
struct tree *child[TREE_NUM_CHILDREN];
int key;
};
#define TREE_EMPTY (0)
/* free all elements of a tree, replacing it with TREE_EMPTY */
void treeDestroy(struct tree **root);
/* insert an element into a tree pointed to by root */
void treeInsert(struct tree **root, int newElement);
/* return 1 if target is in tree, 0 otherwise */
/* we allow root to be modified to allow for self-balancing trees */
int treeContains(struct tree **root, int target);
/* delete target from the tree */
/* has no effect if target is not in tree */
void treeDelete(struct tree **root, int target);
/* pretty-print the contents of a tree */
void treePrint(const struct tree *root);
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <limits.h>
#include "tree.h"
/* free all elements of a tree, replacing it with TREE_EMPTY */
void
treeDestroy(struct tree **root)
{
/* we want to avoid doing this recursively, because the tree might be deep */
/* so we will repeatedly delete the root until the tree is empty */
while(*root) {
treeDelete(root, (*root)->key);
}
}
/* rotate child in given direction to root */
void
treeRotate(struct tree **root, int direction)
{
struct tree *x;
struct tree *y;
struct tree *b;
/*
* y x
* / \ / \
* x C <=> A y
* / \ / \
* A B B C
*/
y = *root; assert(y);
x = y->child[direction]; assert(x);
b = x->child[!direction];
/* do the rotation */
*root = x;
x->child[!direction] = y;
y->child[direction] = b;
}
/* link operations for top-down splay */
/* this pastes a node in as !d-most node in subtree on side d */
static inline void
treeLink(struct tree ***hook, int d, struct tree *node)
{
*hook[d] = node;
/* strictly speaking we don't need to do this, but it allows printing the partial trees */
node->child[!d] = 0;
hook[d] = &node->child[!d];
}
/* splay last element on path to target to root */
static void
treeSplay(struct tree **root, int target)
{
struct tree *t;
struct tree *child;
struct tree *grandchild;
struct tree *top[TREE_NUM_CHILDREN]; /* accumulator trees that will become subtrees of new root */
struct tree **hook[TREE_NUM_CHILDREN]; /* where to link new elements into accumulator trees */
int d;
int dChild; /* direction of child */
int dGrandchild; /* direction of grandchild */
/* we don't need to keep following this pointer, we'll just fix it at the end */
t = *root;
/* don't do anything to an empty tree */
if(t == 0) { return; }
/* ok, tree is not empty, start chopping it up */
for(d = 0; d < TREE_NUM_CHILDREN; d++) {
top[d] = 0;
hook[d] = &top[d];
}
/* keep going until we hit the key or we would hit a null pointer in the child */
while(t->key != target && (child = t->child[dChild = t->key < target]) != 0) {
/* child is not null */
grandchild = child->child[dGrandchild = child->key < target];
#ifdef DEBUG_SPLAY
treePrint(top[0]);
puts("---");
treePrint(t);
puts("---");
treePrint(top[1]);
puts("===");
#endif
if(grandchild == 0 || child->key == target) {
/* zig case; paste root into opposite-side hook */
treeLink(hook, !dChild, t);
t = child;
/* we can break because we know we will hit child == 0 next */
break;
} else if(dChild == dGrandchild) {
/* zig-zig case */
/* rotate and then hook up child */
/* grandChild becomes new root */
treeRotate(&t, dChild);
treeLink(hook, !dChild, child);
t = grandchild;
} else {
/* zig-zag case */
/* root goes to !dChild, child goes to dChild, grandchild goes to root */
treeLink(hook, !dChild, t);
treeLink(hook, dChild, child);
t = grandchild;
}
}
/* now reassemble the tree */
/* t's children go in hooks, top nodes become t's new children */
for(d = 0; d < TREE_NUM_CHILDREN; d++) {
*hook[d] = t->child[d];
t->child[d] = top[d];
}
/* and put t back in *root */
*root = t;
}
/* return 1 if target is in tree, 0 otherwise */
int
treeContains(struct tree **root, int target)
{
treeSplay(root, target);
return *root != 0 && (*root)->key == target;
}
/* insert an element into a tree pointed to by root */
void
treeInsert(struct tree **root, int newElement)
{
struct tree *e;
struct tree *t;
int d; /* which side of e to put old root on */
treeSplay(root, newElement);
t = *root;
/* skip if already present */
if(t && t->key == newElement) { return; }
/* otherwise split the tree */
e = malloc(sizeof(*e));
assert(e);
e->key = newElement;
if(t == 0) {
e->child[LEFT] = e->child[RIGHT] = 0;
} else {
/* split tree and put e on top */
/* we know t is closest to e, so we don't have to move anything else */
d = (*root)->key > newElement;
e->child[d] = t;
e->child[!d] = t->child[!d];
t->child[!d] = 0;
}
/* either way we stuff e in *root */
*root = e;
}
/* delete target from the tree */
/* has no effect if target is not in tree */
void
treeDelete(struct tree **root, int target)
{
struct tree *left;
struct tree *right;
treeSplay(root, target);
if(*root && (*root)->key == target) {
/* save pointers to kids */
left = (*root)->child[LEFT];
right = (*root)->child[RIGHT];
/* free the old root */
free(*root);
/* if left is empty, just return right */
if(left == 0) {
*root = right;
} else {
/* first splay max element in left to top */
treeSplay(&left, INT_MAX);
/* now paste in right subtree */
left->child[RIGHT] = right;
/* return left */
*root = left;
}
}
}
/* how far to indent each level of the tree */
#define INDENTATION_LEVEL (2)
/* print contents of a tree, indented by depth */
static void
treePrintIndented(const struct tree *root, int depth)
{
int i;
if(root != 0) {
treePrintIndented(root->child[LEFT], depth+1);
for(i = 0; i < INDENTATION_LEVEL*depth; i++) {
putchar(' ');
}
printf("%d (%p)\n", root->key, (void *) root);
treePrintIndented(root->child[RIGHT], depth+1);
}
}
/* print the contents of a tree */
void
treePrint(const struct tree *root)
{
treePrintIndented(root, 0);
}
#ifdef TEST_MAIN
int
main(int argc, char **argv)
{
int i;
const int n = 10;
struct tree *root = TREE_EMPTY;
if(argc != 1) {
fprintf(stderr, "Usage: %s\n", argv[0]);
return 1;
}
for(i = 0; i < n; i++) {
assert(!treeContains(&root, i));
treeInsert(&root, i);
assert(treeContains(&root, i));
treePrint(root);
puts("===");
}
/* now delete everything */
for(i = 0; i < n; i++) {
assert(treeContains(&root, i));
treeDelete(&root, i);
assert(!treeContains(&root, i));
treePrint(root);
puts("===");
}
treeDestroy(&root);
return 0;
}
#endif
Makefile. The file speedTest.c can be used to do a simple test of the efficiency of inserting many random elements. On my machine, the splay tree version is about 10% slower than the AVL tree for this test on a million elements. This probably indicates a bigger slowdown for treeInsert itself, because some of the time will be spent in rand and treeDestroy, but I was too lazy to actually test this further.
More information
For more details on splay trees, see the original paper, or any number of demos, animations, and other descriptions that can be found via Google.
Scapegoat trees
Scapegoat trees are another amortized balanced tree data structure. The idea of a scapegoat tree is that if we ever find ourselves doing an insert at the end of a path that is too long, we can find some subtree rooted at a node along this path that is particularly imbalanced and rebalance it all at once at a cost of O(k) where k is the size of the subtree. These were shown by Galperin and Rivest (SODA 1993) to give O(log n) amortized cost for inserts, while guaranteeing O(log n) depth, so that inserts also run in O(log n) worst-case time; they also came up with the name “scapegoat tree”, although it turns out the same data structure had previously been published by Andersson in 1989. Unlike splay trees, scapegoat trees do not require modifying the tree during a search, and unlike AVL trees, scapegoat trees do not require tracking any information in nodes (although they do require tracking the total size of the tree and, to allow for rebalancing after many deletes, the maximum size of the tree since the last time the entire tree was rebalanced).
Unfortunately, scapegoat trees are not very fast, so one is probably better off with an AVL tree.
Skip lists
Skip lists are yet another balanced tree data structure, where the tree is disguised as a tower of linked lists. Since they use randomization for balance, we describe them with other randomized data structures.
Implementations
AVL trees and red-black trees have been implemented for every reasonable programming language you’ve ever heard of. For C implementations, a good place to start is at http://adtinfo.org/.




