Memoization and Dynamic Programming

The Fibonacci Sequence may be defined recursively by the following formula:

f(0) = 0

f(1) = 1

f(n) = f(n-2) + f(n-1)    for n>1

This leads to a very simple recursive implementation of a method to compute the n‘th member of the Fibonacci sequence:

public static int fib(int n) {
    if (n < 0) throw new IllegalArgumentException();
    if (n == 0 || n == 1)
        return n;
    return fib(n - 2) + fib(n - 1);
}

This method is correct, in the sense that it will compute the correct result.  However, it is not efficient because it violates one of the rules of recursion: specifically, it recomputes the answer to subproblems more than once.

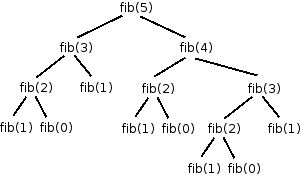
Here is the “tree” of recursive calls that will result from calling the fib method with the argument 5:

Note that the subproblem fib(3) is computed twice, fib(2) is computed three times, fib(1) is computed 5 times, and fib(0) is computed 3 times.  As n increases, the size of the tree (the number of recursive calls required) grows exponentially.  Exponential functions grow very, very fast; so fast that algorithms with exponential running time are generally intractable, even for relatively small input sizes.  In an algorithm with exponential running time, even a small input may require a very large number of steps to solve.

Here is a Java program that computes members of the Fibonacci sequence recursively using the naive approach:

public class Fib {
  public static void main(String[] args) {
    int n = Integer.parseInt(args[0]);
    long begin = System.currentTimeMillis();
    int result = fib(n);
    long end = System.currentTimeMillis();
    System.out.println("fib("+n+")=" + fib(n) + "[" + (end-begin) + " ms]");
  }

  public static int fib(int n) {
    if (n == 0 || n == 1)
      return n;
    else
      return fib(n-2) + fib(n-1);
  }
}

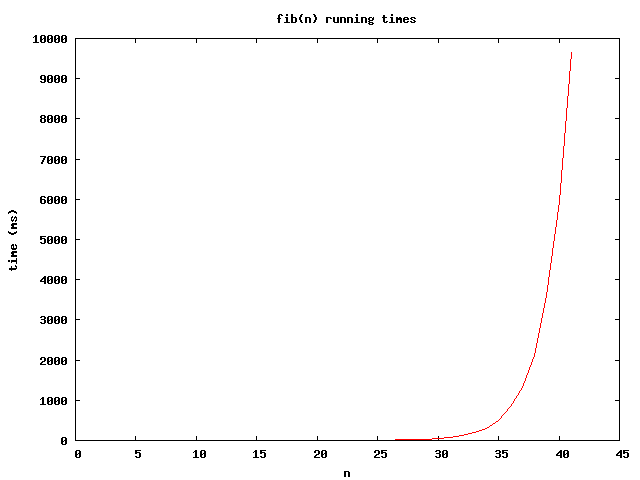
If you try running this program, you will notice that the number of milliseconds required to compute the requested Fibonacci number grows very quickly.  On my laptop^†, the 40th Fibonacci number takes about 6 seconds to compute, and the 41st takes 9.5 seconds!  Here is a graph showing the number of milliseconds required for n=1 to n=41:

^† This was written in 2005. A more recent computer would be faster, but the shape of the plot’s curve would be similar.

Obviously, this is not a good implementation of fib.

Memoization is a technique for avoiding recomputing the answers to subproblems in a recursive algorithm.  The idea is very simple: record the answers to subproblems in a table.  Each time an answer to a subproblem is needed, consult the table.  If no answer exists in the table, perform the computation and save the answer in the table.  Future occurrences of the subproblem can be “solved” by just loading the answer from the table.

Here is a simple memoized version of the same program.  Answers to subproblems are saved in an array called memo.

public class FibMemo {
  public static void main(String[] args) {
    int n = Integer.parseInt(args[0]);
    long begin = System.currentTimeMillis();
    int result = fib(n);
    long end = System.currentTimeMillis();
    System.out.println("fib("+n+")=" + fib(n) + "[" + (end-begin) + " ms]");
  }

  public static int fib(int n) {
    return fibMemo(n, new int[n + 1]);
  }

  public static int fibMemo(int n, int[] memo) {
    if (n == 0 || n == 1)
      return n;

    int answer = memo[n];
    if (answer == 0) {
      answer = fibMemo(n-2, memo) + fibMemo(n-1, memo);
      memo[n] = answer;
    }

    return answer;
  }
}

Because each subproblem is computed only once, this version of fib has linear (O(n)) running time. As you can see, this memoized implementation is a trivial modification of the naive recursive implementation.

A related technique, called dynamic programming, is to start with the smallest subproblem, and then to iteratively work up towards larger problems, until the overall problem is solved.  This kind of solution can be written using a loop of the general form

for j = 1 to n
    memo[j] = solve subproblem j

return memo[n]

The step that reads “solve subproblem j” may be implemented by looking up the answers to previously solved subproblems.

Here is a dynamic programming version of the program to compute the n‘th Fibonacci number:

public class FibDynamic {
  public static void main(String[] args) {
    int n = Integer.parseInt(args[0]);
    long begin = System.currentTimeMillis();
    int result = fib(n);
    long end = System.currentTimeMillis();
    System.out.println("fib("+n+")=" + fib(n) + "[" + (end-begin) + " ms]");
  }

  public static int fib(int n) {
    int[] memo = new int[n+1];
    memo[0] = 0;
    memo[1] = 1;
    for (int i = 2; i <= n; i++) {
      memo[i] = memo[i-2] + memo[i-1];
    }
    return memo[n];
  }
}