Books / Graph Algorithms / Chapter 2
Graph Representation using Adjacency Matrix
The most common way to visually represent graphs is by drawing them. A drawing of a graph maps each vertex to a point in the plane (typically drawn as a small circle or some other shape) and each edge to a curve or straight line segment between the two vertices.
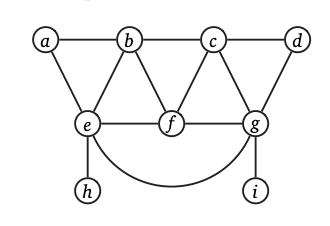
Figure 1: An example graph representation
In computer science, graphs are usually represented by one of two standard data structures: adjacency matrices and adjacency lists. At a high level, both data structures are arrays indexed by vertices; this requires that each vertex has a unique integer identifier between 1 and V. In a formal sense, these integers are the vertices.
Adjacency Matrix
The adjacency matrix of a graph G is a square-matrix of 0’s and 1’s with a row for every vertex. It’s often represented as a two-dimensional array in computer programs. A[u][v] is 1 if there is an edge from u to v, otherwise it is 0. (In weighted graphs, if A is numeric valued, then A[u][v] would be the weight of the edge (u,v).)
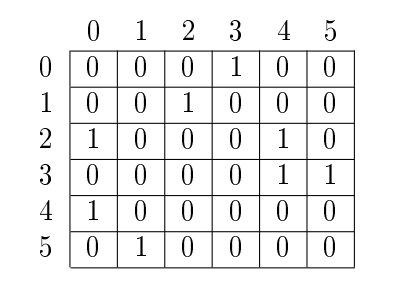
The following asymmetric boolean matrix represents the directed graph shown below.
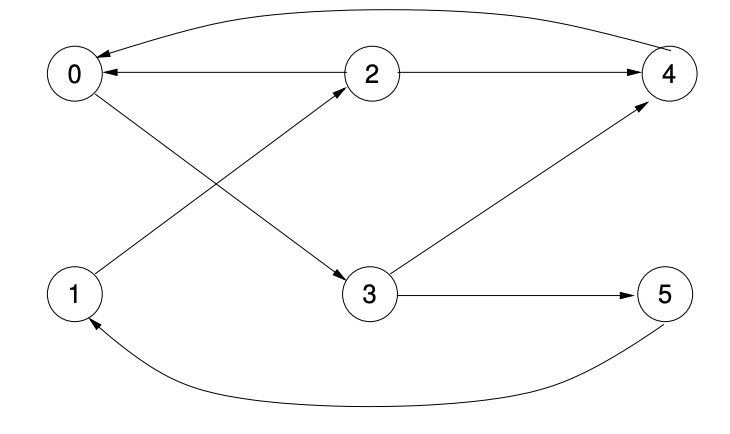
Figure 2: A directed graph used.
For undirected graphs, the adjacency matrix is always symmetric, meaning A[u, v] = A[v, u] for all vertices u and v, because uv and vu are just different names for the same edge, and the diagonal entries A[u, u] are all zeros. For directed graphs, the adjacency matrix may or may not be symmetric, and the diagonal entries may or may not be zero. Here’s another adjacency matrix for a graph where vertices are labelled a, b, c through m.
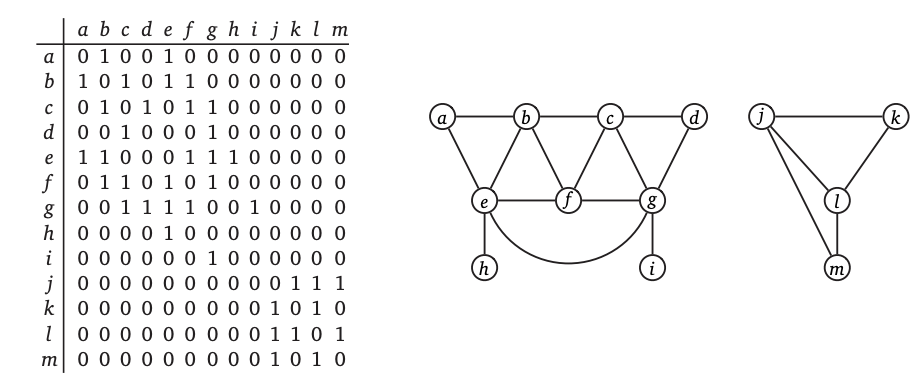
Figure 3: Graph represented as Adjacency Matrix
Code Example of Adjacency Matrix in Java
Advantage of Adjacency Matrix
- It is a very simple representation.
- Given an adjacency matrix, we can decide in O(1) time whether two vertices are connected by an edge just by looking in the appropriate slot in the matrix.
Disadvantages of Adjacency Matrix
- Graphs are usually sparse, meaning that they have lots of zeros. There are \(N^{2}\) entries in a matrix of N vertices, but the number of edges may only be a multiple of N
- Many problems that have efficient solutions cannot be solved efficiently when this representation is used, because they will all tend to be \(O\left(N^{2}\right)\).




