Books / Graph Algorithms / Chapter 5
Topological Sort of a Directed Acyclic Graph
In this chapter
The figure below shows a snapshot of the prerequisites for computer science courses at a Computer Science college.

Figure 1: Topological Sort of a Directed Acyclic Graph of Computer Science Courses and their Pre-requisites
Most students will immediately realize that the set of courses required for the computer science major together with the prerequisite relation is a directed, and hopefully acyclic, graph. That is, if \(c_{1}\) and \(c_{2}\) are nodes in a graph that represent two difference courses, and there is a directed edge from \(c_{1}\) to \(c_{2}\), then it means that \(c_{1}\) is a prerequisite for \(c_{2}\), and that therefore one cannot take \(c_{2}\) until one has successfully completed \(c_{1}\). So for example, according to Figure 1 , there is a directed path from CS127 to CS415 of length 4 , which means that after completing CS127, one needs at least 4 semesters to complete CS415.
Suppose that you are a very busy person and that you can take just one course in each semester. You seek to assign the numbers \(1,2, \ldots, N\) to the N courses you need to take to graduate with a major in Computer Science with the meaning that the course labeled k is to be taken in semester k. This is an example of a topological sort of the graph of courses. It is a linear, or total, ordering of the nodes of the graph such that, if there is a directed path from a node v to a node w in the graph, then v has a lower number than w in the ordering.
It should be pretty obvious that there are many possible topological sorts of the graph in Figure 1. When two or more nodes in the graph are not related, meaning that there is no directed path from one to the other, then their relative order in the topological sort does not matter and multiple topological sorts of the graph are possible. Any valid topological sort is a solution to the problem. In general, the edge set E in a graph defines a partial ordering relation on the vertices; it is not total. A topological sort imposes a total ordering that is consistent with the underlying partial ordering that the edges define. To make the problem precise now, a topological sort of a graph \(G=(V, E)\) with vertices \(\left\{v_{1}, v_{2}, v_{3}, \ldots, v_{N}\right\}\) is an ordering of the vertices such that if there is a path from \(v_{i}\) to \(v_{j}\) in the graph, then \(v_{i}\) must precede \(v_{j}\) in the ordering. The output of a topological sort of a graph \(G=(V, E)\) is an assignment of the numbers \(1,2, \ldots, N\) to the vertices.
A topological sort is not possible for graphs with cycles. If a graph has cycles, then for any two vertices v and w in a cycle, v precedes w and w precedes v. There is no way to create a sequence because if v precedes w, then w cannot be before v, and vice versa.
The Algorithm
Define the in-degree of a node to be the number of edges incident upon the node. For example, in Figure 1, M121 has in-degree 0 and CS235 has in-degree 3. We now prove that:
If a graph has no cycles, then there is at least one node with in-degree 0.
Proof. Suppose to the contrary that every node has in-degree greater than zero. Pick any node arbitrarily. Pick an edge incident on that node and visit the node at its source. Repeat this procedure of following the edge incident on the node in the reverse direction of the edge. If multiple edges are incident on a node, pick any one arbitrarily. Since every node has at least one such incoming edge, the path so followed is of infinite length, as there is always an edge to follow. But there are finitely many nodes in the graph, so some node must appear twice on this path, which implies that the path contains a cycle.
Let v be any one of the nodes whose in-degree is zero. We assign v the number 1 and reduce the in-degree of all vertices adjacent to v by 1 . Reducing the in-degree of an adjacent node by 1 is like removing the edge from v to the node, so if you were simulating this algorithm on paper with a picture of the graph, it would be best to do so using a pencil with an eraser! Next, we try to find another node whose in-degree is 0 and if we do, we repeat this procedure. If we cannot find a vertex with in-degree 0 but we have not visited every vertex, then there must be a cycle, because it means that every node in the remaining non-empty graph has at least one incoming edge, which means that the remaining graph has a cycle, by Lemma 13 above. The following listing is a pseudocode description of the resulting algorithm.
initialize the in-degrees of all vertices by scanning the adjacency lists
counter = 1;
while there are vertices in V yet to be processed {
let v be any vertex with in-degree == 0;
if no such vertex exists {
return CycleFound
} else {
v.topologicalNumber = counter ++;
for each w that is adjacent to v {
decrement its in - degree by 1
}
}
}
Correctness We want to prove that if there is a path from v to w in the graph, then v is assigned a smaller number than w by the algorithm.
We can argue by induction on the length of a path from v to w. If the path has length 1, then (v, w) is an edge in the graph and w cannot be visited before v because the edge (v, w) will not be removed until v is visited, so in-degree(w) will not be 0 until after v is visited. This implies that the number assigned to w is greater than the number assigned to v.
Suppose that we have proved the claim for all paths of length less than n and let v, w be nodes such that the length of the path from v to w is n > 1. By assumption there is a vertex u such that v,…,u is a path of length n − 1 and (u, w) is an edge. By the hypothesis, the topological number assigned to v is less than the topological number assigned to u, and by the previous argument, the number assigned to u is less than that assigned to w, proving the claim for paths of length n.
Partial Implementation and Walkthrough
The simplest way to implement this algorithm is to use a queue for storing the vertices whose in-degrees are zero. The in-degree of each vertex is computed by reading every adjacency list and incrementing the in-degree of vertex v every time that v appears in the adjacency list of some other vertex. This is O(E) since it looks at each edge once.
Having computed all in-degrees, all vertices with in-degree 0 are enqueued and a loop is entered. In the loop, the front of the queue is removed, it is given a topological number, its successors’ in-degrees decremented, and if 0, they are enqueued. The resulting pseudocode follows.
// Find all nodes with in - degree 0
q.makeEmpty();
for each vertex v in V
if (v.indegree == 0)
q.enqueue(v);
// Start processing with a count of 1
counter = 1;
while (!q.empty()) {
v = q.dequeue(); // v has in - degree 0
v.topologicalNumber = counter++;
for each w that is adjacent to v {
// (v , w ) is an edge in the graph
w.indegree--;
if (w.indegree == 0)
q.enqueue(w);
}
}
if (counter != | V | )
return CycleFound; // or throw an exception
This algorithm requires O(|E| + |V|) time. This is because, in the while-loop, each edge is examined at most once and each vertex is processed at most once. Whichever is larger is what dominates the running time.
Let’s look at an actual example. Suppose we have a graph that we want to topographically sort.
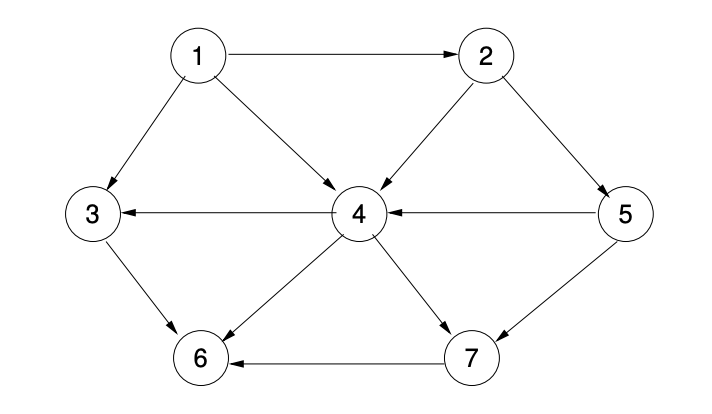
Figure 2: Diagram of a graph to be topologically sorted.
Consider the graph in Figure 1. Two topological orderings of it are 1, 2, 5, 4, 7, 3, 6 and 1, 2, 5, 4, 3, 7, 6. Let us apply the algorithm to it. The in-degrees of all nodes are computed and we see that node 1 has in-degree 0.
We assign a 1 to node 1, and remove edges (1,2), (1,3), and (1,4). Node 2 now has in-degree 0, so we assign 2 to it and remove the edges (2,4) and (2,5). The resulting graph is:
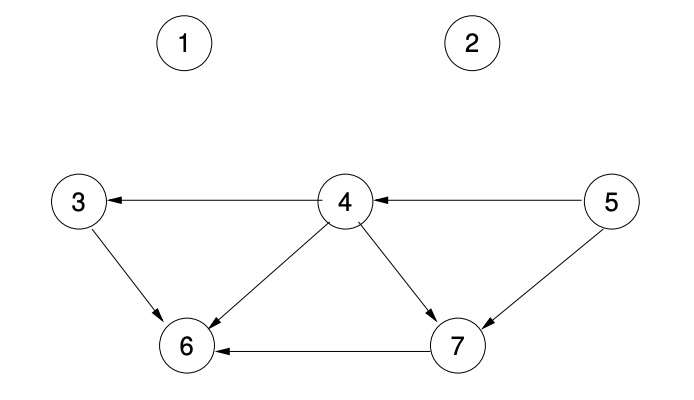
Node 5 now has in-degree 0 so it is assigned 3, and the edges (5,4) and (5,7) are removed. This results in node 4 having in-degree 0, so it is given number 4 and edges (4,3), (4,6), and (4,7) are removed. The graph is now:
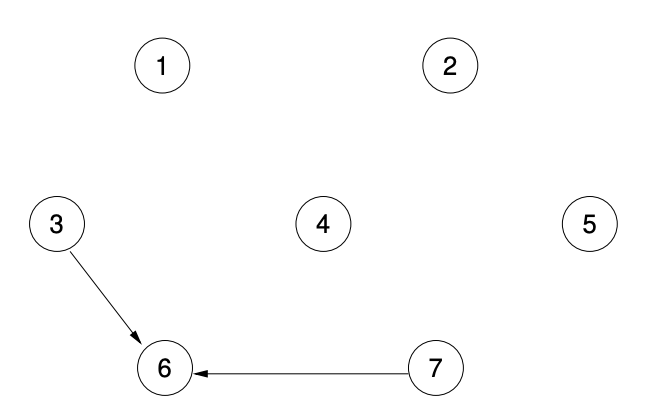
The last few steps assign 3 the number 5, deleting edge (3,6), then assigning number 6 to node 7, deleting (7,6), and assigning 7 to node 6.
For an example of topological sort in Java, please visit this (external) link.




