Books / Graph Algorithms / Chapter 3
Graph Representation using Adjacency Lists
In the previous chapter, we learned that graphs can be represented using Adjacency Matrix. In this chapter, we’ll look at another technique of representing graphs called Adjacency Lists.
By far the most common data structure for storing graphs is the adjacency list because its the most efficient. An adjacency list is an array of lists, each containing the neighbors of one of the vertices (or the out-neighbors if the graph is directed.) In other words, an adjacency list is a linear array with an entry for each vertex, such that each entry is a pointer to a list of vertices adjacent to that vertex.
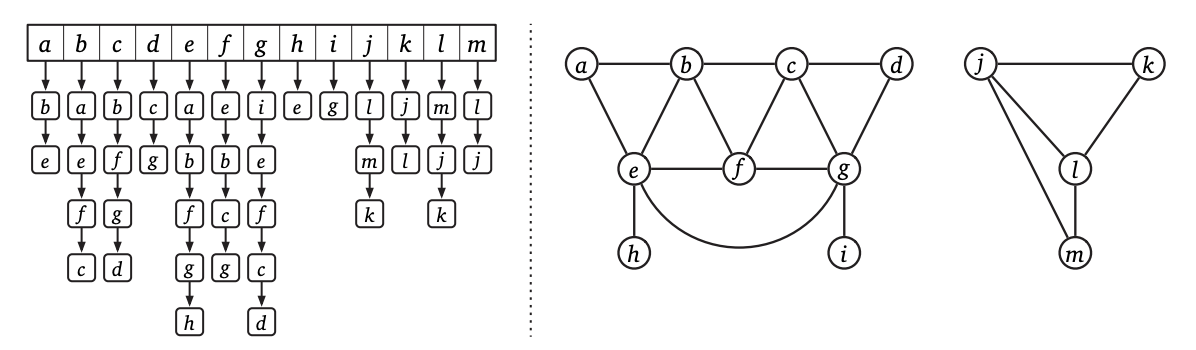
Figure 1: An adjacency list for our example graph
For undirected graphs, each edge uv is stored twice, once in u’s neighbor list and once in v’s neighbor list; for directed graphs, each edge u->v is stored only once, in the neighbor list of the tail u. For both types of graphs, the overall space required for an adjacency list is O(V + E).
There are several different ways to represent these neighbor lists, but the standard implementation uses a simple singly-linked list. The resulting data structure allows us to list the (out-)neighbors of a node v in O(1 + deg(v)) time; just scan v’s neighbor list. Similarly, we can determine whether uv is an edge in O(1 + deg(u)) time by scanning the neighbor list of u. For undirected graphs, we can improve the time to O(1 + min{deg(u), deg(v)}) by simultaneously scanning the neighbor lists of both u and v, stopping either when we locate the edge or when we fall of the end of a list.
Note: Linked lists are not the only data structure we could use; any other structure that supports searching, listing, insertion, and deletion will do.
Adjacency Lists and Weighted Graphs
If the graph is a weighted graph, then the node for each edge in the list would have a member variable that stores the weight.
Adjacency List in Java
Here’s an example of Adjacency List in Java using LinkedLists. In this example, we have 4 nodes: A, B, C and D.
- A has an edge to B.
- B has edges to C and D.
- C has an edge to D.
- D has no edges.
We’ll
import java.util.LinkedList;
// Class to represent a node in the graph
class Node {
String name;
LinkedList<Node> neighbors;
public Node(String name) {
this.name = name;
this.neighbors = new LinkedList<>();
}
}
public class AdjacencyList {
public static void main(String[] args) {
// Create four nodes
Node A = new Node("A");
Node B = new Node("B");
Node C = new Node("C");
Node D = new Node("D");
// Add edges: A -> B,
A.neighbors.add(B);
// B -> C, B -> D
B.neighbors.add(C);
B.neighbors.add(D);
//C -> D
C.neighbors.add(D);
// Put all nodes in an array
Node[] nodes = {A, B, C, D};
// Print the adjacency list
printAdjacencyList(nodes);
}
public static void printAdjacencyList(Node[] nodes) {
for (Node node : nodes) {
System.out.print(node.name + ": ");
for (Node neighbor : node.neighbors) {
System.out.print(neighbor.name + " ");
}
System.out.println();
}
}
}
This prints:
A: B
B: C D
C: D
D:




