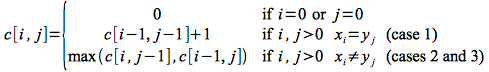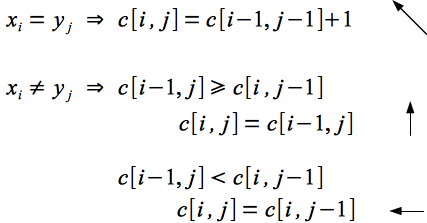To further illustrate using dynamic programming, another problem that can be solved with dynamic programming is finding the longest common subsequence between two sequences.

Sequences

Given a sequence

X = <x₁, x₂, …, x_n>

a sequence of length k

Z = <z₁, z₂, …, z_k>

is a subsequence if there exists a strictly increasing set of indicies <i₁, i₂, …, i_k> such that

In other words, all the elements of Z appear in the same order as they appear in X (but not necessarily consecutively).

For example, consider the seqence X = <A, B, C, B, D, A>. One subsequence is Z = <B, C, D, A> with indices i = <2, 3, 5, 6>.

Longest Common Subsequence

Problem

Given two sequences X of length m and Y of length n as

X = <x₁, x₂, …, x_m>

Y = <y₁, y₂, …, y_n>

find the longest common subsequence (LCS).

Solution

Step 1: Characterize optimality

The brute force procedure would involve enumerating all 2^m subsequences of X (again simply consider all binary strings of length m) and check if they are also subsequences of Y keeping track of the longest one. Clearly this produces exponential run time and does not take advantage of the optimal substructure of the solution.

Define the i^th prefix of a sequence as the first i elements

X_i = <x₁, x₂, …, x_i>

with X₀ representing the empty sequence.

If we assume that Z = <z₁, z₂, …, z_k> is a LCS (with length k) of X and Y then one of the following three cases must hold:

1. If x_m = y_n, then z_k = x_m = y_n and Z_k-1 is a LCS of X_m-1, Y_n-1 . Basically if the last elements of both sequences are the same then it must be the last element of the LCS and the k-1 prefix of the LCS must be a LCS of the m-1 and n-1 prefixes of the original sequences.
2. If x_m ≠ y_n, then if z_k ≠ x_m Z is a LCS of X_m-1, Y. Basically if the last element of the LCS is not the same as the last element of X then it must be a LCS of the prefix of X without the last element.
3. If x_m ≠ y_n, then if z_k ≠ y_n Z is a LCS of X, Y_n-1. Basically if the last element of the LCS is not the same as the last element of Y then it must be a LCS of the prefix of Y without the last element.

In all three cases we see that the LCS of the original two sequences contains a LCS of prefixes of the two sequences (smaller versions of the original problem) ⇒ optimal substructure problem.

Step 2: Define the recursive solution (top-down)

Case 1 reduces to the single subproblem of finding a LCS of X_m-1, Y_n-1 and adding x_m = y_nto the end of Z.

Cases 2 and 3 reduces to two subproblems of finding a LCS of X_m-1, Y and X, Y_n-1and selecting the longer of the two (note both of these subproblems involve also solving the subproblem of Case 1).

Hence if we let c[m,n] be the length of a LCS for X and Y we can write the recursion described by the above cases as

Since each step of the recursion removes at least one element from one of the sequences, there are only Θ(mn) subproblems to consider. Hence we can solve it by creating two tables - C an m x n table storing the LCS lengths and B an m x n table for reconstructing the LCS.

Note that not all subproblems are considered depending on which recursive branch is selected.

Step 3: Compute the length of the LCS (bottom-up)

Replacing m by i and n by j and noting that c[i,0] = c[0,j] = 0, we can rewrite the recursive equation bottom up as follows

When the procedure is complete, the optimal length of the LCS will be stored in c[m,n]. Thus since we fill in the entire table, the procedure will take O(mn).

Step 4: Construct an optimal LCS

Start at any entry containing the max-length (for example c[m,n]) and follow the arrows through the table adding elements in reverse order whenever a ↖ occurs. At worst we move up or left at each step giving a run time of O(m + n).

Alternatively we could avoid the B matrix (saving some space) and reconstruct the LCS from C at each step in O(1) time (using only the surrounding table cells), however it does not provide any improvement in the asymptotic run time.

Example

Consider the two sequences

X = <A, B, C, B, A>

Y = <B, D, C, A, B>

We will fill in the table row-wise starting in the upper left corner using the following formulas

The completed table is given by

i,j		0	1	2	3	4	5
		Y	B	D	C	A	B
0	X	0	0	0	0	0	0
1	A	0	0↑	0↑	0↑	1↖	1←
2	B	0	1↖	1←	1←	1↑	2↖
3	C	0	1↑	1↑	2↖	2←	2↑
4	B	0	1↖	1↑	2↑	2↑	3↖
5	A	0	1↑	1↑	2↑	3↖	3↑

Thus the optimal LCS length is c[m,n] = 3.

Constructing an optimal LCS starting at c[5,5] we get Z = <B, C, B> (added at elements c[4,5], c[3,3], and c[2,1]). Alternatively we could start at c[5,4] which would produce Z = <B, C, A>. Note that the LCS is not unique but the optimal length of the LCS is.

---

---