Books / Analysis of Algorithms / Chapter 27
NP Complete Problems
Last lecture presented the framework for NP-complete problems and showed that there is, in fact, at least one NP-complete problem. Using this one problem, we can show that other problems are also NP-complete using a technique known as reducibility. We can then reduce circuit satisfiability to other problems to show that the other problems are also NP-complete.
Reducibility
In order to show that a new problem is also NP-complete, we will construct a (polynomial time) reduction from an instance of a known NP-complete problem (e.g. circuit satisfiability) to an instance of the new problem. Thus if we could solve the new problem in polynomial time, we could solve the NP-complete problem in polynomial time by simply converting it to an instance of the new problem (in polynomial time), solving the new problem (in polynomial time), and then interpreting the decision result for the NP-complete problem (in polynomial time). Since every problem in NP can be represented as an instance of the original NP-complete problem, if we can show that every instance of the NP-complete problem can be reduced to an instance of the new problem, then the new problem must also be NP-complete (assuming the new problem is ∈ NP itself). This technique has been used to show many interesting problems are NP-complete.
Boolean Satisfiability
Using circuit satisfiability as the initial NP-complete problem, we can show that Boolean satisfiability is NP-complete by reducing any instance of circuit satisfiability to Boolean satsifiability.
Problem
A Boolean expression is a formula composed of
- n Boolean variables x1, x2, …, xn
- m Boolean operations consisting of ∧ (logical AND), ∨ (logical OR), ¬ (logical NOT), → (logical implication), and ⇔ (logical if and only if)
- parentheses
Parentheses delineate clauses that consist of a group of variables that are connected by operands. For example
φ = (( x1 → x2 ) ∨ ¬ (( x1 ⇔ x3 ) ∨ x4 )) ∧ ¬ x2
Clearly an assignment that satisfies this expression is <0, 0, 1, 1>.
It can be shown that Boolean satisifiability is NP-complete by reducing circuit satisfiability to Boolean satisfiability.
Proof
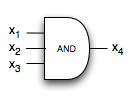
While it would seem intuitive to simply write the Boolean expression for the circuit, this cannot necessarily be done in polynomial time if the gates have fan-out greater than two (i.e. the output of one gate goes to the input of more than 2 other gates). Instead what we do is represent each wire in the circuit by a Boolean variable xi. We then represent each gate by a clause giving the relationship of inputs to output. For example the clause for the following gate
is given by x4 ⇔ ( x1 ∧ x2 ∧ x3 ).
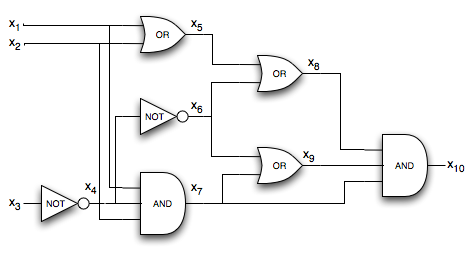
We then construct the Boolean formula by simply AND‘ing all the clauses with the output (which can be done in polynomial time). Clearly both the circuit satisfiability and Boolean satisfiability counterparts have the same resulting decision outputs. For example, the circuit given by
would have the corresponding formula
φ = x10 ∧ ( x4 ⇔ ¬ x3 )
∧ ( x5 ⇔ ( x1 ∨ x2 ))
∧ ( x6 ⇔ ¬ x4 )
∧ ( x7 ⇔ ( x1 ∧ x2 ∧ x4 ))
∧ ( x8 ⇔ ( x5 ∨ x6 ))
∧ ( x9 ⇔ ( x6 ∨ x7 ))
∧ ( x10 ⇔ ( x7 ∧ x8 ∧ x9 ))
Thus if we could solve the Boolean satisfiability problem in polynomial time, we could solve the circuit satisfiablity problem in polynomial time (and by extension any NP problem in polynomial time).
3-CNF Satisfiability
If the Boolean expression consists of exactly 3 OR‘ed variables per clause with all the clauses being AND‘ed, then the expression is said to be in 3-CNF form (conjunctive normal form).
Problem
Given a 3-CNF expression, find an assignment of the literals that satisfies the expression, i.e. causes the expression to evaluate to 1. It can be shown that 3-CNF is also NP-complete by reducing general Boolean satisfiability to 3-CNF.
Proof
The reduction is performed in three steps:
Step 1: Convert clauses into a binary parse tree
Since each Boolean operator is a binary operator, we simply construct a binary parse tree where the nodes are the operators and the literals are leaves. In the case of clauses with multiple literals, we simply add associative paretheses as needed to make binary clauses. We then construct a new expression, similarly to the above reduction from circuit satisfiability to Boolean satisfiability, by AND‘ing the clauses representing each node with the final output.
Step 2: Convert each clause into CNF form
We then construct a truth table for each clause (which contains at most 3 literals) and use the sum-of-products method to create an equivalent Boolean expression that evaluates to 0 in which we have a set of AND‘ed clauses that consist of OR‘ed literals (this is known as DNF form - disjunctive normal form). Finally we negate this expression and apply DeMorgan’s law to convert this expression into the equivalent CNF form that evaluates to 1 if and only if the original expression evaluates to 1.
Step 3: Ensure each clause has exactly 3 literals
Finally we add auxilarly variables p and q as needed to clauses that have less than 3 literals as follows
- If the clause contains 3 literals, then keep it as is
If the clause contains 2 literals, then create two AND‘ed clauses that contain p and ¬ p. In other words, for the clause ( xi ∨ xj ) replace it with
( xi ∨ xj ∨ p ) ∧ ( xi ∨ xj ∨ ¬ p )
Since for any assignment of p, one of the clauses will evaluate to the original and the other will evaluate to 1 (thus not changing the final result of the original expression).
If the clause contains 1 literal, then create four AND‘ed clauses that contain p and ¬ p and q and ¬ q. In other words, for the clause ( xi ) replace it with
( xi ∨ p ∨ q ) ∧ ( xi ∨ ¬ p ∨ q ) ∧ ( xi ∨ p ∨ ¬ q ) ∧ ( xi ∨ ¬ p ∨ ¬ q )
Again since any assignment of p and q will make one of the clauses evaluate to the original and all the others evaluate to 1.
This procedure can be done in polynomial time since the first step adds at most one variable and one clause per operator in the original expression, the second step adds at most 8 clauses (since for 3 literals the truth table has 8 rows), and the third step adds at most 4 clauses. Thus the product of these steps remains a constant factor. Since the procedure basically applies the laws of discrete math, the final 3-CNF expression will be satisifiable if and only if the original Boolean expression is satisfiable.
Example
Consider the Boolean expression
φ = (( x1 → x2 ) ∨ ¬ (( ¬ x1 ⇔ x3 ) ∨ x4 )) ∧ ¬ x2
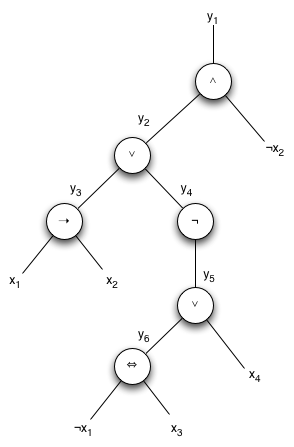
Step 1: Draw binary parse tree
Parse the expression by creating the following output variables of subexpressions:
y6 = ( ¬ x1 ⇔ x3 )
y5 = ( y6 ∨ x4 )
y4 = ( ¬ y5 )
y3 = ( x1 → x2 )
y2 = ( y3 ∨ y4 )
y1 = ( y2 ∧ ¬ x2 )
Making each of the above operators a node gives the following parse tree
Thus the original expression can be rewritten (by traversing the parse tree) as
φ’ = y1 ∧ ( y1 ⇔ ( y2 ∧ ¬ x2 ))
∧ ( y2 ⇔ ( y3 ∨ y4 ))
∧ ( y3 ⇔ ( x1 → x2 ))
∧ ( y4 ⇔ ( ¬ y5 ))
∧ ( y5 ⇔ ( y6 ∨ x4 ))
∧ ( y6 ⇔ ( ¬ x1 ⇔ x3 ))
Step 2: Convert each clause to CNF
Constructing the truth table for the first clause φ’1 = y1 ⇔ ( y2 ∧ ¬ x2 )) gives
y1 y2 x2 (y1 ⇔ (y2 ∧ ¬x2)) 0 0 0 1 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 0
Thus we can write ¬ φ’1 by simply AND‘ing the literals (negating any false values) for each row that evaluates to 0 and OR‘ing all the 0 rows (i.e. sum-of-products) giving
¬ φ’1 = ( ¬ y1 ∧ y2 ∧ ¬ x2) ∨ ( y1 ∧ ¬ y2 ∧ ¬ x2) ∨ ( y1 ∧ ¬ y2 ∧ x2) ∨ ( y1 ∧ y2 ∧ x2)
Finally we can compute the CNF form φ”1 = ¬ ( ¬ φ’1 ) and using DeMorgan’s laws to convert AND to OR giving
φ”1 = ( y1 ∨ ¬ y2 ∨ x2) ∧ ( ¬ y1 ∨ y2 ∨ x2) ∧ ( ¬ y1 ∨ y2 ∨ ¬ x2) ∧ ( ¬ y1 ∨ ¬ y2 ∨ ¬ x2)
For the clause φ’4 = ( y4 ⇔ ( ¬ y5 )) the truth table would be
y4 y5 (y4 ⇔ ¬y5)) 0 0 0 0 1 1 1 0 1 1 1 0
The sum-of-products for ¬ φ’4 gives
¬ φ’4 = ( ¬ y4 ∧ ¬ y5 ) ∨ ( y4 ∧ y5 )
The CNF form for φ”4 = ¬ ( ¬ φ’4 ) gives
φ”4 = ( y4 ∨ y5 ) ∧ ( ¬ y4 ∨ ¬ y5 )
Step 3: Ensure each clause has exactly 3 literals
Clearly all the clauses in φ”1 contain three literals, so that clause is unchanged. However for φ”4, the two clauses only contain 2 literals. Thus we add an auxilary variable p to both of them giving
φ”’4 = ( y4 ∨ y5 ∨ p ) ∧ ( y4 ∨ y5 ∨ ¬ p ) ∧ ( ¬ y4 ∨ ¬ y5 ∨ p ) ∧ (¬ y4 ∨ ¬ y5 ∨ ¬ p )
Also note that the very first clause in φ’ only contains one literal ( y1) so we expand using auxilary variables p and q giving
φ”’0 = ( y1 ∨ p ∨ q ) ∧ ( y1 ∨ ¬ p ∨ q ) ∧ ( y1 ∨ p ∨ ¬ q ) ∧ ( y1 ∨ ¬ p ∨ ¬ q )
In this manner we convert the original expression into one that contains AND‘ed clauses each with exactly 3 OR‘ed literals.
Thus if we could solve 3-CNF in polynomial time we could solve general Boolean satisfiability in polynomial time (and by extension any NP problem in polynomial time).
Clique
The next NP-complete problem we will explore is a graph problem known as clique. For an undirected graph G, a clique is a subset of vertices that form a complete subgraph (i.e. a subset of vertices with every possible edge between all the vertices).
Problem
Given a graph G, find the clique with maximal size, i.e. the complete subgraph with the most vertices. Since this is an optimization problem, we cast it into a decision problem by asking if on a graph there is a clique of size k. It can be shown that the clique problem is NP-complete by reducing 3-CNF to an instance of clique.
Proof
The proof of the reduction from 3-CNF to clique is very interesting because it takes a Boolean expression and converts it into an equivalent graph even though the problems seem to stem from different mathematical domains. Again the proof is constructive. Assume that the 3-CNF expression has k clauses. We then construct a graph such that if the 3-CNF expression is satisfiable, then there will be a clique on the graph of size k.
Step 1: Add vertices to the graph
For each clause, add a vertices in the graph for each literal or negated literal (since each clause has exactly 3 literals there will be 3 vertices per clause in the graph giving a total of 3k vertices in the final graph).
Step 2: Add edges between vertices
Add edges between vertices under the following conditions
- The two vertices come from different clauses
- The vertices are not negations of each other
Using this procedure, it can be shown that if there is an assignment of literals for the 3-CNF formula then those literals will produce a clique of size k. Since at least one literal (or its negation) must be assigned 1 in the expression, these vertices will form a clique in the graph. Conversely, if there is a clique of size k then the clique will contain the literals that satisfy the 3-CNF formula. Since there are no edges between vertices from the same clause, assigning the vertices in the clique to 1 will give a satisfying assignment.
Example
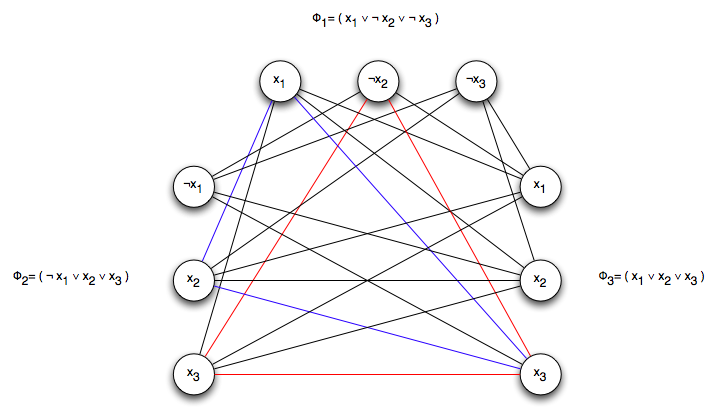
Consider the following 3-CNF expression
φ = ( x1 ∨ ¬ x2 ∨ ¬ x3 ) ∧ ( ¬ x1 ∨ x2 ∨ x3 ) ∧ ( x1 ∨ x2 ∨ x3 )
(clearly a satisfiable assignment is < 0/1, 0, 1>). The graph for the above expression is (with the size 3 clique shown in red)
Note that another clique (indicated in blue) of size 3 would give the assignment <1, 1, 1> which also satisfies the 3-CNF expression.
Thus if we could solve clique in polynomial time we could solve 3-CNF in polynomial time (and by extension any NP problem in polynomial time).