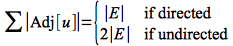---

layout: default title: “Lecture 15: Graph Theory” —

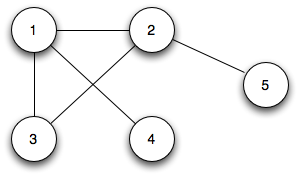
This lecture will be a brief review of terminology from graph theory that will be used for the algorithms in subsequent lectures. We assume that a graph G(V,E) is represented as a pair of finite sets where V is the set of vertices and E is the set of edges.

Directed Graph (digraph)

In a directed graph, the edges are represented by ordered pairs of vertices (u, v) and shown diagramatically as directed arrows (a vertex may be connected to itself via a self-loop).

An edge (u, v) is incident from (i.e. leaves) u and is incident to (i.e. enters) v. If a graph contains an edge (u, v), then v is adjacent to u and is represented notationally as u → v. Note v being adjacent to u does not imply that u is adjacent to v unless edge (v, u) ∈ E. Thus (u, v) and (v, u) are distinct edges in a directed graph.

We say that u and v are neighbors if either (u, v) ∈ E or (v, u) ∈ E.

For each vertex we define the out-degree as the number of edges leaving the vertex, in-degree as the number of edges entering a vertex, and the degree as out-degree + in-degree (i.e. total number of edges at the vertex). If a vertex has degree = 0, then the vertex is isolated.

If the directed graph has no self-loops, then it is a simple directed graph.

Undirected Graph

In an undirected graph, the edges are represented by unordered pairs of vertices. Thus (u, v) and (v, u) represent the same edge and are shown diagramatically as simply a connecting line (note undirected graphs may not contain self-loops).

An edge (u, v) is incident on u and v, and u and v are adjacent to each other.

The degree is the number of edges incident on a vertex.

To convert an undirected graph into a directed one, simply replace each edge (u, v) with (u, v) and (v, u). Conversely to convert a directed graph into an undirected one, replace each edge (u, v) or (v, u) with (u, v) and remove all self-loops.

Paths

A path of length k from u to u’ is a sequence of vertices <v₀, v₁, …, v_k> with u = v₀, u’ = v_k, and (v_i-1, v_i) ∈ E.

If a path p from u to u’ exists, then u’ is reachable from u (denoted u ↝ u’ if G is a directed graph).

The path is simple if all the vertices are distinct.

A subpath is a contiguous subsequence <v_i, v_i+1, …, v_j> with 0 ≤ i ≤ j ≤ k.

A cycle is a path with v₀ = v_k (and is also simple if all the vertices except the end points are distinct). An acyclic graph is a graph with no cycles.

Connected Components

In an undirected graph, a connected component is a subset of vertices thar are all reachable from each other. The graph is connected if it contains exactly one connected component, i.e. every vertex is reachable from every other.

In a directed graph, a strongly connected component is a subset of mutually reachable vertices, i.e. there is a path between any two vertices in the set.

Special Graphs

A complete graph an undirected graph where all vertices are adjacent to all other vertices, i.e. there are edges between every pair of vertices.

A bipartite graph is an undirected graph that can be partitioned into V₁ and V₂ such that for every edge (u, v) ∈ E either

u ∈ V₁ and v ∈ V₂ OR u ∈ V₂ and v ∈ V₁

i.e. the graph can be separated so that the only edges are between vertices in different subsets.

A forest is an undirected acyclic graph. If it is also connected, then it is a tree.

A directed acyclic graph is known as a DAG.

Graph Representation

Two common methods for implementing a graph in software is either using an adjacency list or an adjacency matrix.

Adjacency List

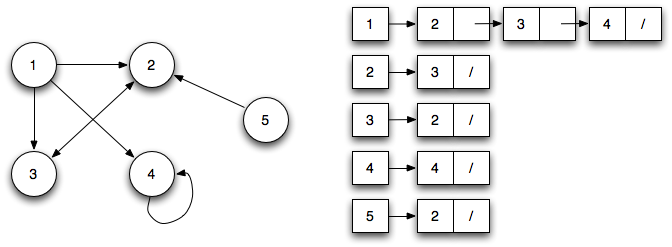
In an adjacency list implementation, we simply store the adjacent vertices (i.e. edges) for each vertex in a linked list denoted Adj[u]. If we sum up the lengths of all the adjacency lists, we get either

⇒ Θ(V + E) storage is required.

This representation is good for sparse graphs where |E| ≪ |V|². One drawback is that to determine if an edge (u, v) ∈ E requires a list search ⇒ Θ(V).

For the original directed graph, the adjacency list would be

Adjacency Matrix

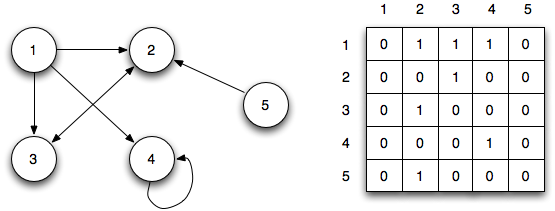
In an adjacency matrix implementation, we store the edges in a VxV matrix A either as binary values or real numbers for weighted edges.

⇒ Θ(V²) storage is required (independent of E).

This representation is good for dense graphs where |E| ≈ |V|². The advantage is it only takes Θ(1) time to determine if an edge (u, v) ∈ E since it is simply a matrix element access. If the graph is undirected, then A = A^T so only the upper triangular half needs to be stored.

For the original directed graph, the adjacency matrix would be

---

---